ラマヌジャンがあるタクシーのナンバーに書かれていた1729をみて、それは、「2つの3乗数の和として2通りに表すことができる最小の自然数」と言ったことがタクシー数の発端です。
ラマヌジャンは、「インドの魔術師」とも呼ばれた天才数学者で、その才能は他の数学者と一線を画しています。難しい数式を何個も発見していています。ラマヌジャンの天才ぶりは啓示によるものじゃないかと思われるぐらい人間離れしています。
1729
\(12^3+1^3=10^3+9^3=1729\)
と2通りに表すことができる数です。このように2通りの3乗和で表せる自然数は1729より小さい数では存在しません。原点中心の曲線\(x^3+y^3=r^3\)を書いた時に、その曲線上の整数格子点の場所を調べることになります。r=12.00231437…の場合に、(1,12),(9,10),(10,9),(12,1)の整数格子点を通るというわけです。下記に表で数値の分布を表しました。
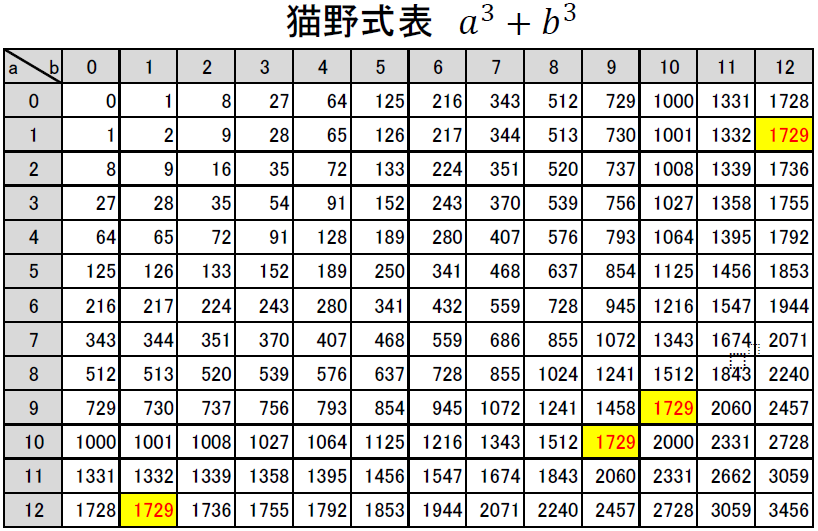
対角線で対象な分布になっていますが、12まで作ったこの表で同じ数がみつかるのは、1729しかありません。
注意
なお、普通タクシー数というのは、\(a^3+b^3=c^3+d^3\)と2通り(当然a=c,b=dなどは省く)の3乗和で表すことができる最小の数のことを言いますが、ここでは、2通り(以上)の3乗和であらわせる数をタクシー数と呼ぶことにします(ローカル定義です)。
50までのタクシー数
50までの3乗数でタクシー数をEXCELを使って求めました。
\(12^3 + 1^3 = 10^3+9^3=1729=7・13・19\)
\(16^3 + 2^3 = 15^3+9^3=4104=2^3・3^3・19\)
\( 24^3 + 2^3 = 20^3+18^3=13832 =2^3・7・13・19\)
\( 27^3 + 10^3 =24^3+ 19^3=20683=13・37・43\)
\( 32^3 + 4^3 = 30^3 + 18^3 = 32832= 2^6・3^3・19\)
\( 34^3 + 2^3 = 33^3 + 15^3 = 39312=2^4・3^3・7・13 \)
\( 34^3 + 9^3 = 33^3 + 16^3 = 40033 =7^2・19・43 \)
\( 36^3 + 3^3 = 30^3 + 27^3 = 46683 = 3^3 7・13・19 \)
\( 39^3 + 17^3 = 36^3 + 26^3 = 64232 = 2^3・7・31・37\)
\( 40^3 + 12^3 = 33^3 + 31^3 = 65728 = 2^6・13・79\)
\( 48^3 + 4^3 = 40^3 + 36^3 = 110656 =2^6・7・13・19\)
\( 48^3 + 6^3 = 45^3 + 27^3 = 110808 =2^3・3^16・19\)
上の3乗和で表せれるを素因数分解すると、5や11はでてきませんね。19がわりとたくさん出ているような気がします。
上記の式から下記をピックアップしました。
\(12^3 + 1^3 = 10^3+9^3=1729=7・13・19\)
\(24^3 + 2^3 = 20^3+18^3=13832 =2^3・7・13・19\)
\(36^3 + 3^3 = 30^3 + 27^3 = 46683 = 3^3 7・13・19 \)
\(48^3 + 4^3 = 40^3 + 36^3 = 110656 =2^6・7・13・19\)
これらは仲間です。例えば、\(12^3 + 1^3 = 10^3+9^3=1729=7・13・19\)
の両辺に\(2^3\)をかけると2番めの式になります。このように、3乗の数を両辺にかけていけばいくらでも二つの三乗和の数が得られますので、これらは除外して考えましょう。
つまり、a,b,c,dは互いに素であるものだけを調べてみます。
すると、素因数分解してでてきた因子は、3,7,13,19,31,37,43
タクシー数は、3mod4の因子が多いですが、でてきてもよさそうな11や23が現れていませんし、11の代わりかどうかわかりませんが、1mod4の13がでてきています。mod4での分類ではだめなのでしょうか。mod8で分類でしょうか。
素因数分解して因数調べてみました。わずかな例でみてるだけですが、でてくる素数とでてこない素数があるようです。さらなる研究が必要です。
コメント
1729に関しての情報追加。桁ごとに分解して10を作るには、\(7+9/(1+2)\)とすればできます。
負の数をつかってもよいのなら、91=63+(-5)3 =43+33があります。キャブタクシー数と呼ばれています。
3通りの和になる数をみつけるためにはもっと大きな数まで計算しないと見つかりません。

