 代数
代数 純虚数について簡単な例での説明
複素数の中でも、実数部がないものを純虚数と言います。一般に複素数は、虚数単位を\(i\)とした時、\(a+bi\)(ここで\(a,b\)は実数)という形で表すことができます。この場合、\(a\)の部分を実部(実数部)、\(b\)の部分を虚部...
 代数
代数 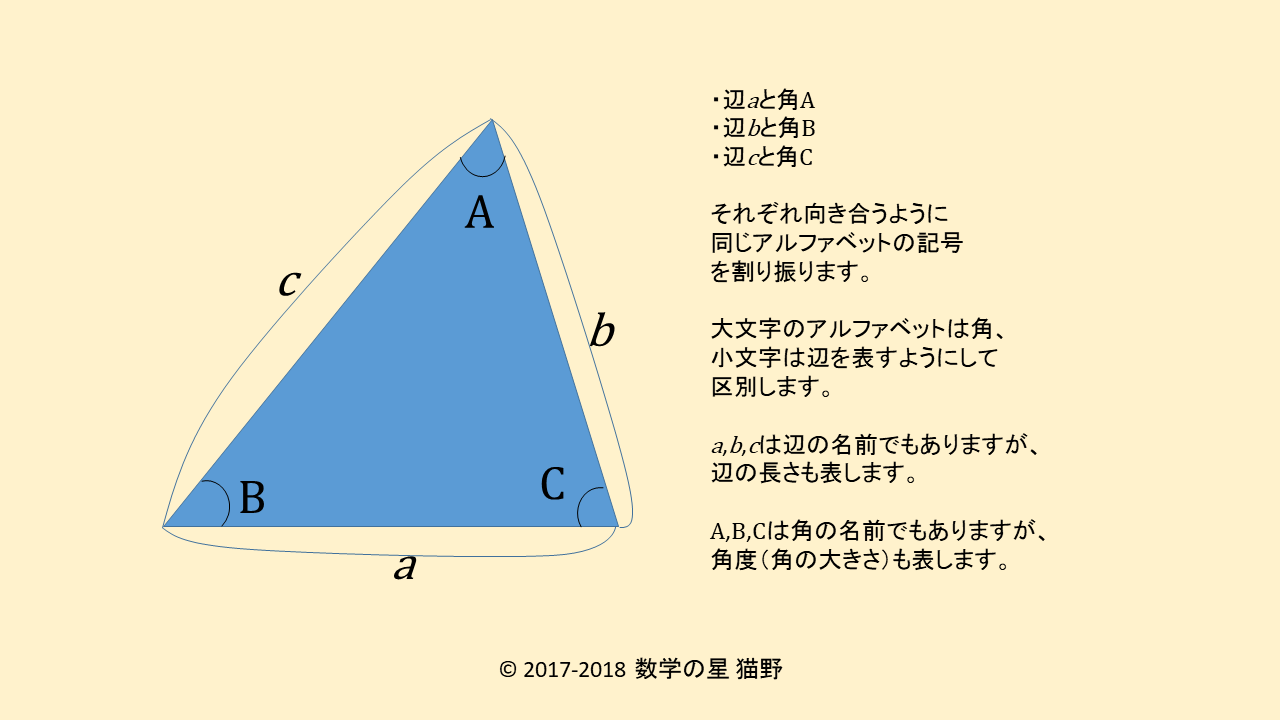 数学問題
数学問題 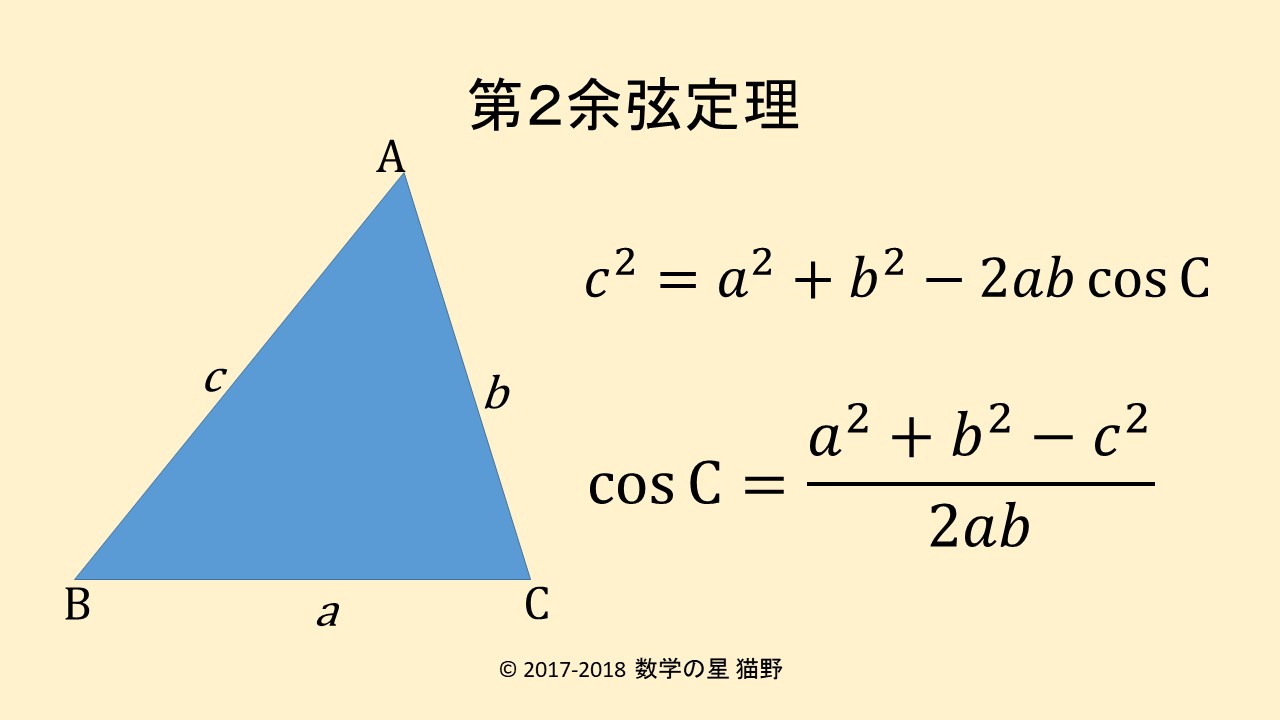 代数
代数  三次体
三次体  三次体
三次体  数論
数論  数学問題
数学問題  数論
数論  集合論
集合論  猫野の微分積分
猫野の微分積分