[msg#wsiki]
問題
\(\displaystyle f(x)=x+\frac{1}{2}-\frac{1}{2}|x-1|\)とする。
xを実数とし、
\(x_1=f(x),\\x_2=f(x_1),\\\cdots,\\x_n=f(x_{n-1})\)
とするとき、数列
\(\{x_n\}\)
が収束するようなxの範囲とそのときの
\(\displaystyle \lim_{x \rightarrow \infty} x_n\)
を求めよ。
解き方
まず、関数に絶対値が入っていて扱いにくいのでxの反映で場合分けして絶対値のない定義で書き表します。
x>1のとき
\(\displaystyle f(x)=x+\frac{1}{2}-\frac{1}{2}(x-1)\)
\(\displaystyle f(x)=\frac{1}{2}x+1\)
x≦1のとき
\(\displaystyle f(x)=x+\frac{1}{2}+\frac{1}{2}(x-1)\)
\(\displaystyle f(x)=\frac{3}{2}x\)
となる。
まとめると数列{xn}は、
\begin{eqnarray}
x_{n+1} =
\begin{cases} \displaystyle \frac{3}{2}x_n & ( x_n \le 1 ) \\
\displaystyle \frac{1}{2}x_n+1 & ( x_n \gt 1 )
\end{cases}
\end{eqnarray}
と定義される。
解答
(1)1<xの時
1<xnであるから、\(\displaystyle x_{n+1}=\frac{1}{2}x_n+1\)と考えて良い。
このとき、
\(\displaystyle x_{n+1}-2=\frac{1}{2}(x_n-2)\)
より、\(x_n -2\rightarrow 0\)
であるから、\(x_n \rightarrow 2\)
(2)0<x≦1の時
最初の項に対しては、xn≦1であるから、
\(\displaystyle x_{n+1}=\frac{3}{2}x_n\)の関係でxnは決まっていく。
xnは単調に増加していき、ある時点から1を超える。
そこからさきは、\(\displaystyle x_{n+1}=\frac{1}{2}x_n+1\)に則ってxnは決まっていくから、
結局は(1)の場合に帰着して、
\(x_n \rightarrow 2\)
となる。
(3)x=0の時
x=0である場合は、任意のnに対して、
\(\displaystyle x_{n}=0\)
よって、
\(x_n \rightarrow 0\)
となる。
(4)x<0の時
任意のnにたいして、xn<0であるから、
\(\displaystyle x_{n+1}=\frac{3}{2}x_n\)の関係でxnは決まっていく。
これは、公比3/2の等比数列であるから、発散する。
上記の場合分けをまとめると、
答え
0≦xの時に収束し、
\(\displaystyle \lim_{x \rightarrow \infty} x_n=2\; (0<xの時)\)
\(\displaystyle \lim_{x \rightarrow \infty} x_n=0\; (x=0の時)\)
である。
コメント
x>1のとき
\(x_{n+1}=\frac{1}{2}x_n+1 \)
x≦1のとき
\(x_{n+1}=\frac{3}{2}x_n \)
と勘違いすると収束するxの範囲を間違えてしまう。
他の数列の極限に関する問題:数列の極限の問題一覧
[ad#foot]
猫野の解析は

鉄則微分・積分
をテキストとして使っています。
鉄則ゼミ7の問題を解いています。
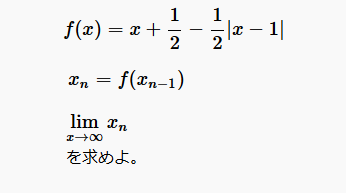


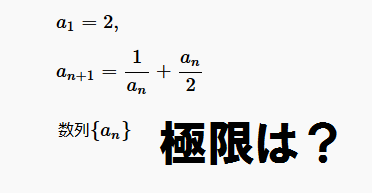
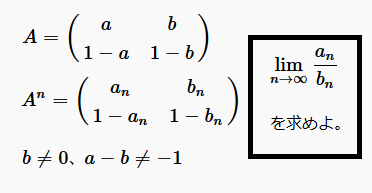
コメント