微分の定義がよくわかっていないと解けない(解けたと言えない)問題です。
「猫野の微分積分」の記事一覧
積分にでてくる∫やdxの記号の意味
積分の式は、\(\displaystyle \int(xの関数)dx\)という形で書かれます。 この\(\int\)と\(dx\)の記号は慣れないとなかなか読み解けないものです。 記号の意味や解釈はいろいろありますが、こ […]
超難問√tan(x)の不定積分と定積分の解き方
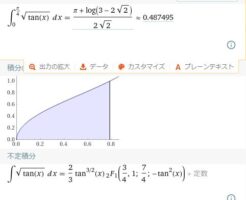
関数\(\sqrt{\tan(x)}\)の積分です。 微分と比較にならないほど積分ははるかに難しいです。 まずは、素敵なウルフラムの計算結果を参照してください。 https://www.wolframalpha.com/ […]
関数√tan(x)を微分するとこうなる
関数\(\sqrt{\tan(x)}\)の微分です。 関数\(\sqrt{\tan(x)}\)の微分(導関数) \(\sqrt{\tan(x)}\)の微分は、 \(\sqrt{f(x)}\)の微分公式を使って計算します。
定積分と不定積分の違い
定積分も不定積分もどちらも略して積分と呼ばれますので混乱します。 そこで、定積分と不定積分の違いを例をもって説明します。 不定積分 ある関数f(x)を微分してf'(x)になったとします。 このとき、f(x) […]
微分の記号dy/dxは分数扱いしてよいのか
y=f(x)といった関数があったとします。 微分の書き方として、 y’ f'(x) \(\displaystyle \frac{dy}{dx} \) \(\displaystyle \frac{df}{dx} […]
数学者寺田文行先生の命日です
寺田文行教授 寺田文行(てらだぶんこう)先生は、元早稲田大学理工学部教授でした。 1927年静岡県生まれ。専門は整数論でした。 2016年3月3日に89歳でお亡くなりになったそうです。 本日は命日です。 鉄則シリーズで学 […]
漸化式の極限は求めた後で証明する。収束性が不明なので。
まずは、次の漸化式の問題の答えを考えてください。 問題 次の数列の極限値を求めよ。 \( a_1=1, a_{n+1}=\sqrt{a_n+2} \) 問題の解説 \( a_{n […]
導関数の意味から使い方をマスターする!
「微分する」って言うのは、「導関数を求める」こと。 「導関数を求める」ってのは、 「傾きを示す関数を求める」ってこと。 何の「傾き」っていうかというと、 関数をグラフで書いた時、その接線の傾き […]