[msg#wsiki]
問題
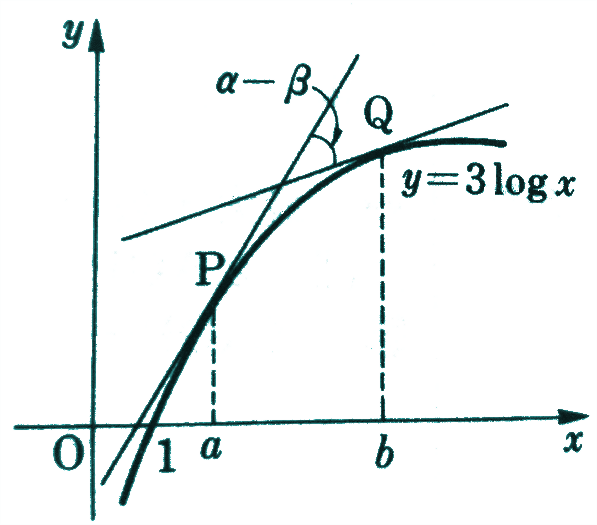
曲線\(y=3 \log x\)の上の2点\(P,Q\)の\(x\)座標をそれぞれ\(a,b\)とし、\(a<b\)とする。
\(P,Q\)におけるこの曲線の2つの接線のなす鋭角が45°で、
\(a,b\)がともに整数であるとき、\(a,b\)を求めよ。
解答(解き方)
まず、図を書いて問題の意図を把握します。
\(a,b\)がともに整数というのは、一旦わすれ、鋭角が45°となるための\(a,b\)の条件を求め、整数解を求めます。
鋭角(角度)が45°というのを式で表すのが難しいですが、傾きを正接(タンジェント(tangent))で表し、角度の差が45°であることを加法定理から導きます。
\(P,Q\)における接線の傾きの角度をそれぞれ\(α、β\)とします。
\(0°≦α,β≦90°\)となるようにできます。
傾きは微分係数で表すことができ、
\(y=3 \log x\)から、
\(y^\prime = \frac{3}{x}\)
ですから、
\(\displaystyle \tan α = \frac {3}{a} \)
\(\displaystyle \tan β = \frac {3}{b} \)
\(a<b\)であることに注意すると、
\(3/a>3/b\)ですから、
\( \tan α > \tan β \)
したがって、\(α>β\)でなければならず、
問題文より、\(α-β=45°\)となります。
\(\displaystyle \tan (α-β)=\frac{\tan α – \tan β}{1+\tan α \tan β}\)
\(\displaystyle =\frac{3/a – 3/b}{1+(3/a)(3/b)}\)
\(\displaystyle =\frac{3b – 3a}{ab+9}\)
\(\displaystyle =\tan{45°} =1\)
\(\displaystyle {3b – 3a} ={ab+9}\)
となるような整数a,bを求めれば、それが答えとなります。
上記の式を変形すると、
\(\displaystyle (a-3)(b+3)=-18\)
となりますが、a>0, b>0を考えると、aは1または2に絞り込まれます。
\(a=1のとき、b=6\)
\(a=2のとき、b=15\)
となり、a,bが整数になる解となるため、2組の答えが得られます。
\((a=1,b=6)\)
\((a=2,b=15)\)
答え
\(a=1,b=6\) と \(a=2,b=15\)
[ad#foot]
その他の問題: 関数の極限に関する問題 数列の極限の問題一覧 数列の極限に関する問題2
[ad#nekob]




コメント