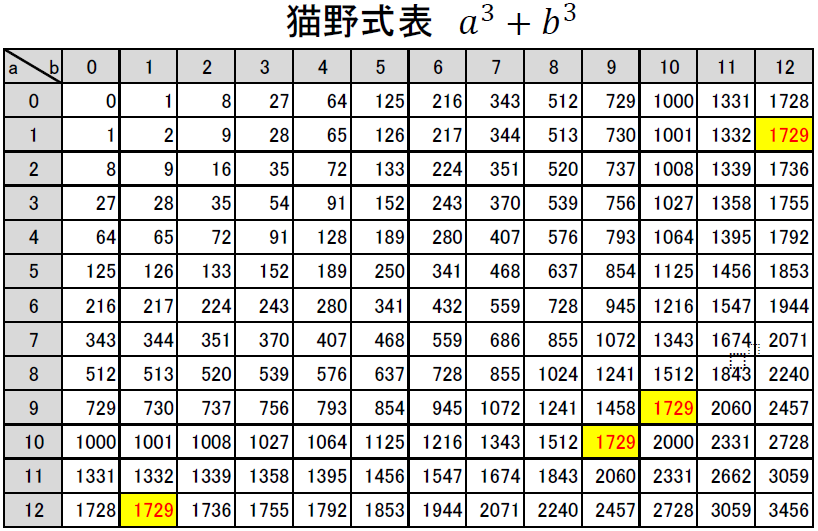
代数 タクシー数である２通り以上の３乗和を素因数分解した数の研究
天才数学者ラマヌジャンのタクシー数の研究 で２通りの３乗和で表すことのできる自然数を求め、素因数分解したときに、でてくる素因数がかなり限定的だったのがきになって、もう少し大きい数でも調べてみました。２通りの３乗和で表すことのできる自然数２通...
猫野 流星
代数 代数 2009年一橋大学タクシー数を求める問題
タクシー数に関する入試問題問題２以上の整数n,mは、\(n^3+1=m^3+10^3\)を満たす。m,nを求めよ。(２００９年の一橋大学前期の数学問題より)解答例整数に関する不定方程式です。素因数分解し、有限個の分解によって場合分けし解を絞...
代数 天才数学者ラマヌジャンのタクシー数の研究
ラマヌジャンがあるタクシーのナンバーに書かれていた１７２９をみて、それは、「２つの３乗数の和として２通りに表すことができる最小の自然数」と言ったことがタクシー数の発端です。ラマヌジャンは、「インドの魔術師」とも呼ばれた天才数学者で、その才能...
数論 複雑な２次の因数分解でもたすき掛け不要！
たすき掛けで因数分解したくても、適した数が見つからない！２次の因数分解の話ですが、「たすき掛けで因数分解できない！」こんなことありませんか？たすき掛けのやり方は習って知っている、でも、答えが見つからない！例えば、\(6x^2-11x+4\)...
代数 平方根(ルート)の近似値を計算する方法
√iなどの複素数の平方根については、「複素数の平方根を求める公式と使用例」を参照ください。√２を求めよ√２は無理数ですので、√2を実数(小数表示)で表すと、1.4142・・・と無限小数となります。この、無理数√2の1.4142・・・はどうや...
代数 複素数の平方根(ルート)を求める公式と使用例
数式の展開に時間がかかります。ご容赦ください。先に、結論となる公式を書いておきます。b≧0の時\(\displaystyle \sqrt{a+bi}\\=\pm \left( \sqrt{\frac{a + \sqrt{a^2+b^2}}...
代数 注意！二次方程式の解の公式が使えない
2次方程式の解の公式\(ax^2+bx+c=0,(a \ne 0)\)という\(x\)に関する2次方程式の解\(x\)は、\で与えられる。というのが解の公式と呼ばれるものです。式の形を覚えるのに苦労しますが、完全に覚え使いこなせるようになる...
代数 最大公約数を求める最強ツールはユークリッドの互除法
ユークリッドの互除法最強です。アルゴリズムの威力をしるためのツールでもあります。原理は実に簡単なのですが、このツールによって、いろいろな整数の性質がわかってきます。整数論するには省けない最強ツールなのです。ユークリッドの互除法とは、a,bを...
代数 算数からはじまる素数
素数との出会い小学校の５年生のときに素数をならった覚えがあります。その時の授業はかなり印象的でした。今振り返ると、考える授業といってもよいと思う授業でした。不思議だったのです。５年のあるとき、先生が突然素数をもとめる授業を行ったのです。素数...
数論 円周率の日に円周率の計算
３月１４日は？ホワイトデー！、それよりも重要な日、円周率の日です！本日は円周率の日円周率の計算方法は他数あれど、有名なのは、arctan()を使う方法（その中でも特にマチンの公式）。しかし、それよりも単純で、効率的な方法が。その名は、ガウス...