 猫野の微分積分
猫野の微分積分 sinとcosの対称式は、t=sin(x)+cos(x)とおくとよい
問題\(\displaystyle f(x)=\frac{1}{\sin x}+\frac{1}{\cos x} \left( 0 < x < \frac{\pi}{2}\right)\)の最小値を求めよ。解答(解き方)微分の計算がややこし...
 猫野の微分積分
猫野の微分積分 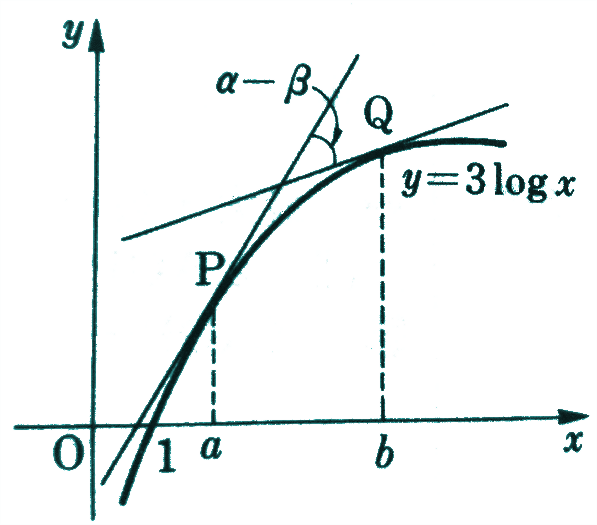 猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分 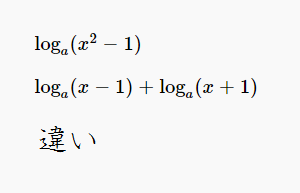 解析
解析  猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分 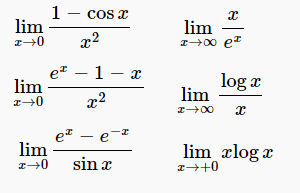 猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分 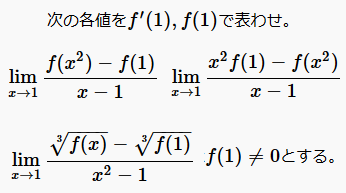 猫野の微分積分
猫野の微分積分