相加平均相乗平均(AM-GM不等式)
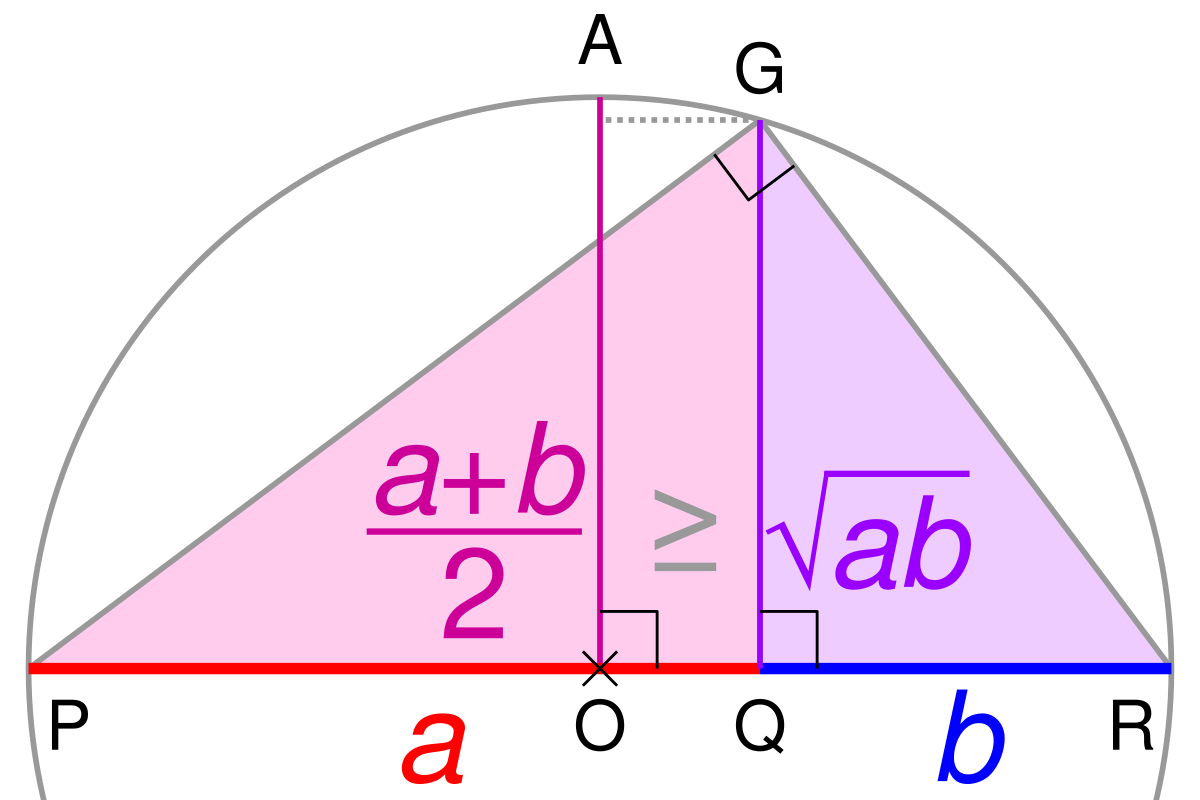
相加平均≧相乗平均の関係の不等式は、AM-GM不等式と書かれることもよくあります。
AMというのは、算術平均、GMというのは相乗平均（幾何平均）の略です。AMとGMの関係を表す不等式なので、AM-GM不等式と書かれるわけです。
超有名なこのAM-GM不等式ですが、その証明はめちゃくちゃたくさん発掘されていて、またそのどれもが奥深く興味が尽きない不等式です。数学的帰納法の例題としても使いましたが、ここでの証明方法は、
https://en.wikipedia.org/wiki/Inequality_of_arithmetic_and_geometric_means
でも紹介されている方法です。つまり、有名な証明の中の一つです。
別解
さて、例題では、n=5の場合のAM－GM不等式を証明しています。ここでも、n=5の場合の別解を示します。
証明すべき不等式を改めてかくと、
\(a_1,a_2,a_3,a_4,a_5>0\)のとき、
\(\frac{a_1+a_2+a_3+a_4+a_5}{5}\ge \sqrt[5]{a_1 a_2 a_3 a_4 a_5}\)
が成立する。
この不等式を証明したのですが、途中で、\(A=\frac{a_1+a_2+a_3+a_4+a_5}{5}\)と置くところがポイントでした。つまり、左辺をAとおいて証明ができたのですが、逆に「右辺をGとおいて証明できないか？」というのがここでの問いです。
結論をいうと、その方法でも似たように証明できます。
概略を書くと、
\(G=\sqrt[5]{a_1 a_2 a_3 a_4 a_5}\)とおくと、
\(G=\sqrt[8]{a_1 a_2 a_3 a_4 a_5 G^3}\)である。
n=8の相加平均相乗平均の証明が既知とすると、
\(\frac{a_1+a_2+a_3+a_4+a_5+G+G+G}{8} \ge \sqrt[8]{a_1 a_2 a_3 a_4 a_5 G^3}=G\)
左辺のGを右辺に移行すると、もとめる不等式が得られます。
不等式の両辺を8乗しなくてすむところがAとおいて証明するよりいいかも。
AM-GM不等式について
超有名な不等式AM-GM不等式。
これだけで本ができると思います。それぐらい、応用が大きく、なおかつ美しさを感じる不等式です。
ある不等式が、AM-GM不等式を使うと魔法のように証明できてしまうことも多々あります。
数の本質を感じる不等式なわけです。不等式はすべてAM-GM不等式に帰着されるのではないかと思うほどです。ちょっと、これは言い過ぎかもしれませんが、それほど威力がある不等式なのです。
私の一番好きな不等式です。
[ad#foot]
