[msg#wsiki]
問題
次の関数の増減・極値と凹凸を調べ、グラフをかけ。
(1)\(\displaystyle f(x)=\frac{(x-1)^2}{x^2+1}\)
(2)\(\displaystyle f(x)=\frac{x}{\log x}\)
解答(解き方)
グラフは、微分の応用の最高峰です。
微分を計算することで、関数のグラフの概略がわかり、またグラフから最大値・最小値を把握することができます。
特に、公式を使えば微分が求めれる関数ですので、微分し極値を求めていきます。
極値を求めるために方程式を解く必要があります。ここがすんなり求められないと難しくなります。
凹凸も調べるため、微分は2回行います。
商の微分公式
\(\displaystyle \left(\frac{f(x)}{g(x)}\right)^{\prime} = \frac{f^{\prime}(x)g(x)-f(x)g^{\prime}(x)}{g(x)^2}\)
増減の判定
- f'(x)=0の場合、極値
- f'(x)>0の場合、(狭義の意味で)単調増加
- f'(x)<0の場合、(狭義の意味で)単調減少
凹凸(上に膨らんでいるか下に膨らんでいるか)の判定
- f”(x)=0の場合、変曲点(上に凸から下に凸に変わる、もしくは下に凸から上に凸に変わる点)
- f”(x)>0の場合、下に凸(∪)
- f”(x)<0の場合、上に凸(∩)
(1)
まず、与えられた関数を微分します。
\(\displaystyle f^{\prime}(x)=\frac{2(x-1)(x^2+1)-(x-1)^2(2x)}{(x^2+1)^2}\)
\(\displaystyle =\frac{ (2x^3+2x-2x^2-2) – (2x^3-4x^2+2x) }{(x^2+1)^2}\)
\(\displaystyle =\frac{ 2x^2-2 }{(x^2+1)^2}\)
\(\displaystyle =\frac{ 2(x-1)(x+1) }{(x^2+1)^2}\)
うまく、導関数が因数分解できる関数でした。
\(\displaystyle x=-1,1\)で極値を取ります。
さらに微分します。
\(\displaystyle f^{\prime \prime}(x)=\frac{ 4x(x^2+1)^2 -(2x^2-2)(2(x^2+1)2x) }{(x^2+1)^4}\)
\(\displaystyle =\frac{ 4x(x^2+1) -(2x^2-2)(4x) }{(x^2+1)^3}\)
\(\displaystyle =\frac{ – 4x^3+12x }{(x^2+1)^3}\)
\(\displaystyle =\frac{ – 4x(x^2-3) }{(x^2+1)^3}\)
こちらもうまく因数分解できました。
\(\displaystyle x=0,-\sqrt{3},\sqrt{3}\)で変曲点を取ります。
増減表を書くと
| \(x\) | -\(\infty\) | \(-\sqrt{3}\) | -1 | 0 | 1 | \(\sqrt{3}\) | \(\infty\) | ||||||
| \(f(x)\) | 1 | \( \nearrow\) |
2 | \( \searrow\) |
0 | \( \nearrow\) |
1 | ||||||
| \(f'(x)\) | + | 0 | – | 0 | + | ||||||||
| \(f”(x)\) | + | 0 | – | 0 | + | 0 | – | ||||||
±∞のところも極限値も求められるので計算し正確なグラフにします。
(2)
logの真数条件から定義域は暗に\(0<x\)です。
\(\displaystyle f^{\prime}(x)=\frac{\log x – x (1/x)x}{(\log x)^2}\)
\(\displaystyle =\frac{\log x -1}{(\log x)^2}\)
\(x=e\)で極値を取ることがわかりました。
\(\displaystyle f^{\prime \prime}(x)=\frac{(1/x) (\log x)^2 – (\log x -1)((2{\log x})(1/x)}{(\log x)^4}\)
\(\displaystyle =\frac{ \log x /x- 2(\log x -1)/x} {(\log x)^3}\)
\(\displaystyle =\frac{ – \log x +2} {x(\log x)^3}\)
\(x=e^2\)で変曲点を取ることがわかりました。
分母がゼロにならない点を考えることも必要ですが、分母の符号も気にする必要があります。
\(\displaystyle \lim_{x\rightarrow +0}\frac{x}{\log x}=0\)
となることも計算しておきます。
増減表を書くと
| \(x\) | 0 | 1 | 1 | e | e | e^2 | \(\infty\) | ||||
| \(f(x)\) | →0 | \( \nearrow\) |
未 | \( \searrow\) |
0 | \( \nearrow\) |
1 | ||||
| \(f'(x)\) | – | 未 | – | 0 | + | ||||||
| \(f”(x)\) | – | 未 | + | 0 | – | ||||||
※未:定義されない(未定義)
答え
(1)
\(\displaystyle f^{\prime}(x)=\frac{ 2(x-1)(x+1) }{(x^2+1)^2}\)
\(\displaystyle f^{\prime \prime}(x) =\frac{ – 4x(x^2-3) }{(x^2+1)^3}\)
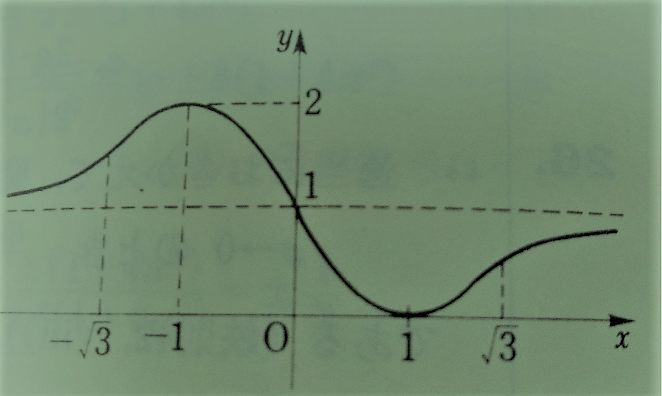
グラフtz030_1
(2)
\(\displaystyle f^{\prime}(x)=\frac{\log x -1}{(\log x)^2}\)
\(\displaystyle f^{\prime \prime}(x)=\frac{ – \log x +2} {x(\log x)^3}\)
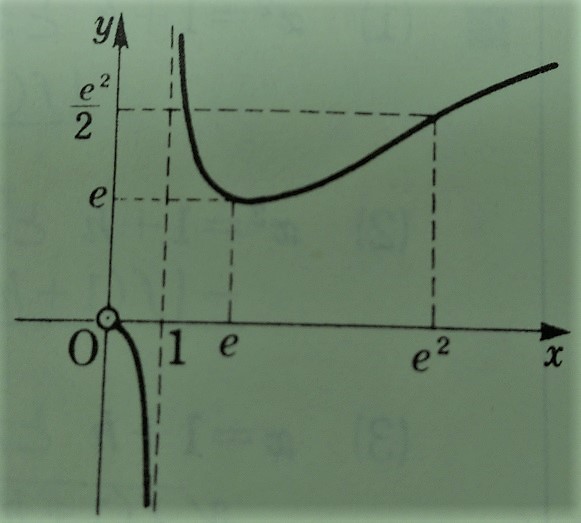
グラフ
[ad#foot]
その他の問題: 関数の極限に関する問題 数列の極限の問題一覧 数列の極限に関する問題2
[ad#nekob]




コメント