[msg#wsiki]
問題
ABを直径とする半径1の半円周上の動点をP,Qとする。
AP=PQを満たす四角形APQBの面積の最大値とそのときのBQの長さを求めよ。
解答(解き方)
四角形APQBの面積をなんらかのパラメータを使って表し、パラメータがどの値の時に最大値となるかを考えます。
この問題の場合、(半)円の中心をOとして、角POAをθとした時に、θで面積を表すと簡単な式が得られます。
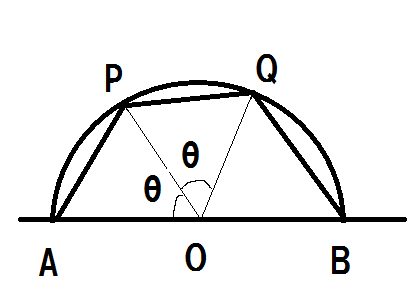
簡単といっても、三角関数を使うので、ある程度の計算力は必要ですが、長さをパラメータにして面積を表すのにくらべると、格段にシンプルな式となります。
三角形の面積の公式
三角形ABCがあって、角ABCをθとすると、三角形ABCがの面積Sは、
\(\displaystyle S=\frac{1}{2} \overline {AB} \, \overline {BC} \sin θ\)
2辺の長さとその挟む角のsinで面積が求められるわけですね。
この公式を使うと、
四角形APQBの面積をSとするとSは、
三角形AOP+三角形POQ+三角形QOBですから、
半径=1であることから
\(\displaystyle 1=\overline{AO}=\overline{OP}=\overline{QO}=\overline{OQ}\)
に注目すれば、
\(\displaystyle S=\frac{1}{2} \sin θ + \frac{1}{2} \sin θ + \frac{1}{2} \sin ({\pi-2θ})\)
\(\displaystyle = \sin θ + \frac{1}{2} \sin {2θ}\)
したがって、
\(\displaystyle 0<θ<\frac{\pi}{2}\)
の範囲でSの最大値を求めれば、答えが得られます。
ここまでくれば、あとは微分の問題となります。
微分して、極値をもとめ、最大値を導き出します。
Sをθで微分すると、
\(\displaystyle S’=\cos θ+ \cos{2θ} \)
\(\displaystyle S’=\cos θ+ 2\cos^2{θ}-1 \)
倍角の公式を使っています。
\(\displaystyle \cos 2θ\\
= \cos^2 θ-\sin^2 θ \\
=2 \cos^2 θ-1\\
=1-2 \sin^2 θ\)
\(\displaystyle S’=(2\cos θ-1)(\cosθ+1) \)
うまい具合に因数分解できます。
ここで因数分解できないと、迷宮入りしてしまうのですが、
問題の図から、直感的に
\(\displaystyle θ=\frac{\pi}{3}\)
のときに最大になりそうだとあたりを付け、
\(\cos \frac{θ}=\frac{1}{2}\)の因数を持つだろうという予測をヒントにできます。
増減表を書くと
| θ | 0 | \(\displaystyle \frac{\pi}{3}\) | \(\displaystyle \frac{\pi}{2}\) | ||
| \(\displaystyle \frac {dS}{dθ}\) | + | 0 | – | ||
| S | 0 | 増加 | 極大\(\displaystyle \frac{3\sqrt{3}}{4}\) | 減少 | 0 |
よって、\(\displaystyle Sは、 θ=\frac{\pi}{3}\)の時に最大となる。
\(\displaystyle S=\sin \frac{\pi}{3} + \frac{1}{2}\sin\frac{2\pi}{3}=\frac{3\sqrt{3}}{4}\)
このとき、三角形QOB、は正三角形となるので、BQ=1となります。
答え
四角形APQBの最大面積は、\(\displaystyle \frac{3\sqrt{3}}{4}\)
そのときのBQの長さは1
[ad#foot]
その他の問題: 関数の極限に関する問題 数列の極限の問題一覧 数列の極限に関する問題2
[ad#nekob]


