問題
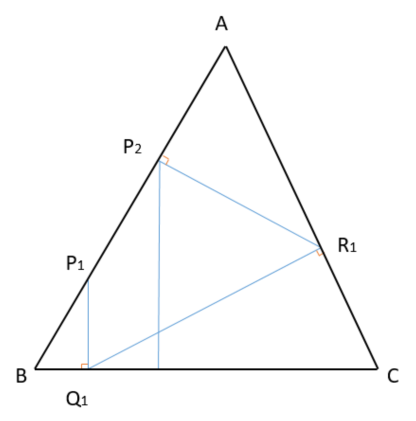
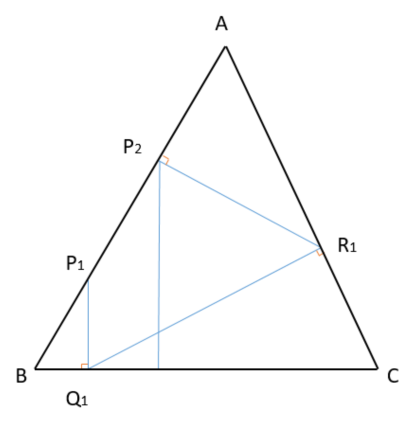
正三角形ABCの辺AB上の1店をP1とする。P1から辺BCへ下ろした垂線の足をQ1、Q1から辺CAに下ろした垂線の足をR1、R1から辺ABへ下ろした垂線の足をP2として、P2からさらに同じ操作を繰り返してQ2、R2、P3、Q3、R3、…とする。
n→∞のとき、Pnはどの点に近づくか。
解き方
APnの長さをXnとし、数列Xnがどのような長さに近づくか調べます。
三角形ABCが正三角形であるので、
三角形、PnBQn、QnCRn、RnAPn+1は、辺の長さが2:1:√3の直角三角形です。
これから、APn、BQn、CRnはわりと簡単に求められます。
正三角形の一辺の長さをaとします。
APn=xnとすると
PnB=a-xn
三角形の比から
BQn=(a-xn)/2
これから
CRn=QnC/2=(a-BQn)/2=(a+an)/4
APn+1=RnA/2=(a-CRn)=(3a-xn)/8
以上より、xn+1=(3a-xn)/8
という漸化式(隣接2項間)が得られました。
この漸化式からxnの極限をもとめれば、Pnの位置がわかります。
解答
APnの長さをXnとすると、
\(AP_n\)の長さを\(x_n\)とすると、
\(\displaystyle x_{n+1}=\frac{3a-x_n}{8}\)である。
これを変形すると、
\(\displaystyle (x_{n+1}-\frac{a}{3})=-\frac{1}{8}(x_{n+1}-\frac{a}{3})\)
数列\(\displaystyle \{x_{n}-\frac{a}{3}\}\)は、
初項\(\displaystyle x_{1}-\frac{a}{3}\)、公比\(\displaystyle -\frac{1}{8}\)の等比数列だから、
一般項は、
\(\displaystyle x_{n}-\frac{a}{3} = \left(x_1-\frac{a}{3}\right) \left(-\frac{1}{8}\right)^{n-1} \)
上記の数列は0に収束するから
\(\displaystyle x_{n}-\frac{a}{3} \rightarrow 0\)
すなわち、
\(\displaystyle x_{n}\rightarrow \frac{a}{3} \)
よって、点PnはABの3等分点でAに近い方の点に近づく。
その他の問題: 数列の極限の問題一覧
[ad#foot]


コメント