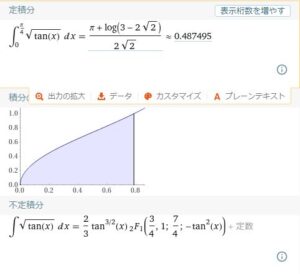
関数\(\sqrt{\tan(x)}\)の積分です。
微分と比較にならないほど積分ははるかに難しいです。
まずは、素敵なウルフラムの計算結果を参照してください。
https://www.wolframalpha.com/input/?i=%E2%88%AB_0%5E%7Bpi%2F4%7Dsqrt%28tan%28x%29%29dx&lang=ja
わずか数秒でこのような計算をしてしまうWolframAlphaに敬意を表します。
使用道具
ありとあらゆる公式を駆使します。
- 置換積分
- 部分積分
- 三角関数の公式
関数\(\sqrt{\tan(x)}\)の不定積分
まずは、\(\sqrt{\tan(x)}\)の不定積分を求めます。
見やすくするため、積分定数は省略して書いています。
ルートやtanを消す
\(\displaystyle \int{\sqrt{\tan(x)}dx}\)
この積分は三角関数(tan)の積分ですが、、
\(\displaystyle t=\sqrt{\tan(x)} \)で置換積分すると有理式の積分へ変換することができます。
両辺を2乗してから\(\displaystyle \frac{dt}{dx}\)を求めると計算が少し楽です。
\(\displaystyle t^2=\tan(x)\)
両辺を\(x\)で微分します。
\(\displaystyle \frac{d}{dx}t^2=\frac{d}{dx} \tan(x)\)
\(\displaystyle 2t \frac{dt}{dx}= \frac{1}{\cos(x)^2}\)
\(\displaystyle \cos(x)^2\)
\(\displaystyle \frac{1}{\cos(x)^2}=\frac{\cos^2(x)+\sin^2(x)}{\cos(x)^2}\)
\(\displaystyle =1+\left(\frac{\sin(x)}{\cos(x)}\right)^2\)
\(\displaystyle =1+\tan(x)^2\)
\(\displaystyle =1+t^4\)
を使うと、
\(\displaystyle 2t \frac{dt}{dx}=1+t^4\)
\(\displaystyle dx=\frac{2t}{1+t^4}dt\)
となって、元の積分の式は、
\(\displaystyle 2t \frac{dt}{dx}=1+t^4\)
\(\displaystyle dx=\frac{2t}{1+t^4}dt\)
\(\displaystyle \int{\sqrt{\tan(x)}dx}\)
\(\displaystyle =\int{t \frac{2t}{1+t^4}dt}\)
\(\displaystyle =\int{ \frac{2t^2}{1+t^4}dt}\)
ルート記号も、tan記号も消えた積分になりました。
有理関数の積分計算
有利関数の積分は、まずできるだけ分母の次数を下げた式に変形します。
次数を下げる方法は、変数置換、部分分数分解が基本のやり方となります。
ここで、\(u=t^2\)と置くと次数が下がって簡単になるような気がしますが、
置換してみると
\(\displaystyle \frac{du}{dt}=2t\)より、\(\sqrt{u}\)という計算式も出現し、せっかく消えたルートが復活でこれではうまくいきません。
また\(t\)の符号判定も面倒です。
一見複雑になったように見えますが、ここは部分分数に分解します。
部分分数への展開方法は、地味でひたすら計算するだけですので、ここではその計算過程を書くのは省略し計算結果のみ示します。
\(\displaystyle \frac{t^2}{1+t^4}\)
\(\displaystyle =\frac{1}{2\sqrt{2}}\left(\frac{t}{1-\sqrt{2}t+t^2}-\frac{t}{1+\sqrt{2}t+t^2}\right)\)
このように分母が2次の部分分数に分解することができます。
後で示す有理関数の積分公式が使えるよう、次のように4つ積分式に分けます。
\(\displaystyle \int \frac{2t^2}{1+t^4} dt\)
\(\displaystyle =\int \frac{t}{\sqrt{2}(1-\sqrt{2}t+t^2)} dt \)
\(\displaystyle -\int \frac{t}{\sqrt{2}(1+\sqrt{2}t+t^2)} dt\)
\(\displaystyle =\frac{1}{2\sqrt{2}} \int \frac{ -\sqrt{2}+2y }{1-\sqrt{2}t+t^2} dt \)
\(\displaystyle +\frac{1}{2} \int \frac{1}{1-\sqrt{2}t+t^2} dt\)
\(\displaystyle -\frac{1}{2\sqrt{2}} \int \frac{ \sqrt{2}+2y }{1+\sqrt{2}t+t^2} dt \)
\(\displaystyle +\frac{1}{2} \int \frac{1}{1+\sqrt{2}t+t^2} dt\)
公式が使えるための変形がやっとできました。
次の節で示す公式を使ってさらに計算します。
\(\displaystyle =\frac{1}{2\sqrt{2}} \log|1-\sqrt{2}t+t^2| \)
\(\displaystyle +\frac{1}{\sqrt{2}} \tan^{-1}(\sqrt{2}t-1) \)
\(\displaystyle -\frac{1}{2\sqrt{2}} \log|1+\sqrt{2}t+t^2| \)
\(\displaystyle +\frac{1}{\sqrt{2}} \tan^{-1}(\sqrt{2}t+1) \)
壮絶な計算となりましたが、やっとできました。
\(t=\sqrt{\tan(x)}\)を代入すれば不定積分の完成です(積分定数省略)。
log(自然対数)の部分もまとめます。
\(\displaystyle =\frac{1}{2\sqrt{2}} \log \left| \frac{1-\sqrt{2}t+t^2}{1+\sqrt{2}t+t^2} \right| \)
\(\displaystyle +\frac{1}{\sqrt{2}} \tan^{-1}(\sqrt{2}t-1) \)
\(\displaystyle +\frac{1}{\sqrt{2}} \tan^{-1}(\sqrt{2}t+1) \)
\(\displaystyle =\frac{1}{2\sqrt{2}} \log \left| \frac{1-\sqrt{2\tan(x)}+\tan(x)}{1+\sqrt{2\tan(x)}+\tan(x)} \right| \)
\(\displaystyle +\frac{1}{\sqrt{2}} \tan^{-1} \left(\sqrt{2\tan(x)}-1 \right) \)
\(\displaystyle +\frac{1}{\sqrt{2}} \tan^{-1} \left(\sqrt{2\tan(x)}+1 \right) \)
\(\displaystyle \tan^{-1}(α)+\tan^{-1}(β)=\tan^{-1}\left(\frac{α+β}{1-αβ}\right)\)
を使ってさらにまとめると、最終結論の式
\(\displaystyle \int{\sqrt{\tan(x)}dx}\)
\(\displaystyle =\frac{1}{2\sqrt{2}} \log \left| \frac{1-\sqrt{2\tan(x)}+\tan(x)}{1+\sqrt{2\tan(x)}+\tan(x)} \right| \)
\(\displaystyle +\frac{1}{\sqrt{2}} \tan^{-1} \left( \frac{\sqrt{2\tan(x)}}{1-\tan(x)} \right) \)
を得ることができます。
定積分\(\int_0^{π/4}\sqrt{\tan(x)}\)
不定積分の結果を用いて
定積分\(\displaystyle \int_{0}^{π/4} {\sqrt{\tan(x)}dx}\)
を求めてみます。
不定積分の\(x\)に\(π/4\)と\(0\)を代入して差をとればよいです。
\(\displaystyle \tan(π/4)=1\)
\(\displaystyle \tan(0)=0\)
\(\displaystyle \int{\sqrt{\tan(x)}dx}\)
\(\displaystyle =\frac{1}{2\sqrt{2}} \log \left| \frac{1-\sqrt{2\tan(x)}+\tan(x)}{1+\sqrt{2\tan(x)}+\tan(x)} \right| \)
\(\displaystyle +\frac{1}{\sqrt{2}} \tan^{-1} \left( \frac{\sqrt{2\tan(x)}}{1-\tan(x)} \right) \)
ですから、
\(\displaystyle \int_{0}^{π/4} {\sqrt{\tan(x)}dx}\)
\(\displaystyle =\left[\frac{1}{2\sqrt{2}}\log \left( \frac{2-\sqrt{2}}{2+\sqrt{2}} \right)+\frac{π}{2\sqrt{2}} \right]-\left[\frac{1}{2\sqrt{2}}\log(1)+\tan^{-1}(0)\right]\)
\(\displaystyle =\left[\frac{1}{2\sqrt{2}}\log \left( \frac{2-\sqrt{2}}{2+\sqrt{2}} \right)+\frac{π}{2\sqrt{2}} \right]\)
\(\displaystyle =\frac{1}{2\sqrt{2}}\log \left( \sqrt{2}-1 \right)^2+\frac{π}{2\sqrt{2}} \)
\(\displaystyle =\frac{1}{\sqrt{2}}\log \left( \sqrt{2}-1 \right)+\frac{π}{2\sqrt{2}}\)
注意
\(\displaystyle \tan^{-1} \left(\frac{\sqrt{2\tan(x)}}{1-\tan(x)}\right)\)
に\(x=π/4\)を代入すると、分母が0になってしまうので調整が必要ですが、
ここでは、\(x=0,π/4\)の間の値を考えているので、
\(\displaystyle \tan^{-1} \left( \frac{\sqrt{2\tan(x)}}{1-\tan(x)}\right)=\frac{π}{2}\)としています。
分母が2次の有理関数の積分
分母が2次式である有理関数の積分は、次の2つの形の組み合わせで解きます。
タイプA
\(\displaystyle =\frac{2ax+b}{ax^2+bx+c}\)
という形の分母2次式、分子1次式です。
タイプAの形の場合、次のように積分できます。
\(\displaystyle \int \frac{2ax+b}{ax^2+bx+c}\)
\(\displaystyle =\log |{ax^2+bx+c}|\)
タイプB
\(\displaystyle \frac{d}{ax^2+bx+c}\)
(ただし\(\displaystyle b^2-4ac<0\))
という形の分母2次式、分子定数です。
タイプBの場合は、逆三角関数がでてきます。
\(\displaystyle \int\frac{d}{ax^2+bx+c}\)
\(\displaystyle =\int\frac{d}{a\left(x+\frac{b}{2a}\right)^2+c-\frac{b^2}{4a}}\)
\(\displaystyle = \frac{2d}{\sqrt{4ac-b^2}}\tan^{-1}\left(\frac{2ax+b}{\sqrt{4ac-b^2}}\right)\)
公式としては覚えにくい形ですが、
\(\displaystyle \int\frac{1}{x^2+1} = \tan^{-1}(x)\)
の基本形を知っていれば変数変換で得られます。