 猫野の微分積分
猫野の微分積分 「微分する」ってどういう意味?「導関数」との関係は?
「微分」はなんとなくわかるけど、「微分する」となるとなんだかちんぷんかんぷん。微分って木っ端微塵にしたチリのようだと思うよ、だったら、「微分する」っていうのは、細かく切り刻むことじゃん!\(x^2\)を微分したら\( 2x \)になるという...
 猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分 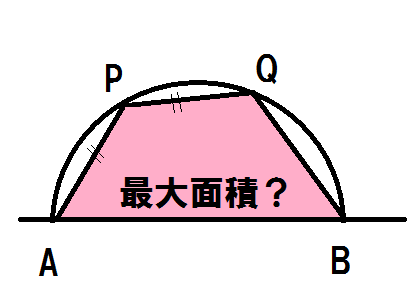 猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分 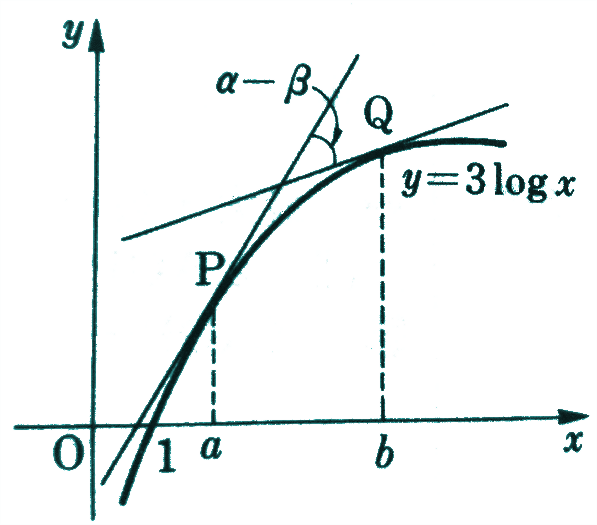 猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分 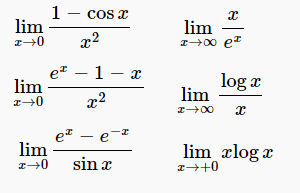 猫野の微分積分
猫野の微分積分