猫野の微分積分 「微分する」ってどういう意味？「導関数」との関係は？
「微分」はなんとなくわかるけど、「微分する」となるとなんだかちんぷんかんぷん。微分って木っ端微塵にしたチリのようだと思うよ、だったら、「微分する」っていうのは、細かく切り刻むことじゃん！\(x^2\)を微分したら\( 2x \)になるという...
猫野の微分積分
猫野の微分積分 猫野の微分積分 微分積分の概念を小学生でもわかりやすく捉えるには
高校で出てくる「微分」と「積分」は、いかにも難しそうな名前ですよね。でも、もし「なんとなく言葉は知っているけど、よくわからない」と思っているなら、これから紹介するお話を読んでみてください。イメージしやすい例を使って、微分と積分の考え方を説明...
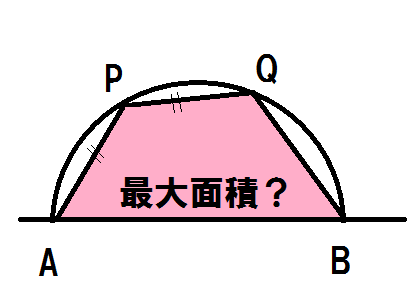
猫野の微分積分 半円に内接するある四角形の最大の面積を求めるの問題
問題ABを直径とする半径１の半円周上の動点をP,Qとする。AP=PQを満たす四角形APQBの面積の最大値とそのときのBQの長さを求めよ。解答（解き方）四角形APQBの面積をなんらかのパラメータを使って表し、パラメータがどの値の時に最大値とな...
猫野の微分積分 次数があってsin,cosの扱いが難しい微分の問題
問題関数\(\displaystyle f(x)=3( \sin x - \cos x) + \cos{2x}\)の最大値を求めよ。解答（解き方）\(\sin x と \cos x\)の対称式ではありませんが、すこし工夫すると対称式の問題と...
猫野の微分積分 sinとcosの対称式は、t=sin(x)+cos(x)とおくとよい
問題\(\displaystyle f(x)=\frac{1}{\sin x}+\frac{1}{\cos x} \left( 0 < x < \frac{\pi}{2}\right)\)の最小値を求めよ。解答（解き方）微分の計算がややこし...
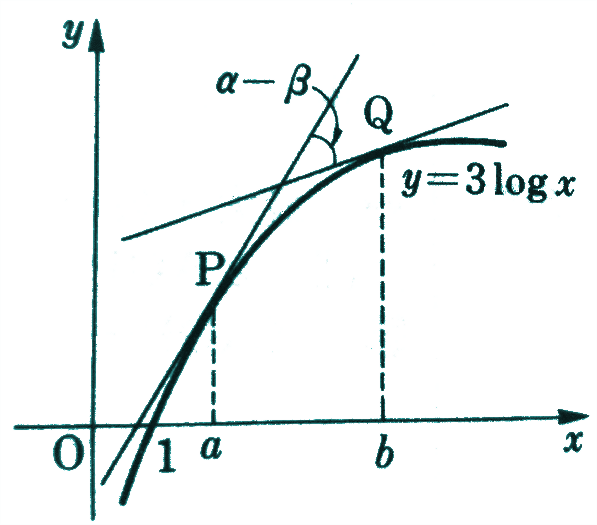
猫野の微分積分 曲線の二つの接線が４５°で交わる条件を求める
問題曲線\(y=3 \log x\)の上の２点\(P,Q\)の\(x\)座標をそれぞれ\(a,b\)とし、\(a<b\)とする。\(P,Q\)におけるこの曲線の２つの接線のなす鋭角が45°で、\(a,b\)がともに整数であるとき、\(a,b...
猫野の微分積分 ある曲線に直行する接線の交点が意外な答えとなる問題
問題点Pから曲線\(y=\sin^2 x (0≦x≦\pi)\)に引いた２つの接線が直行するように点Pの座標を定めよ。解答（解き方）問題をぱっと読むと、求めるPは複数（無限）にあるように思えますが、Pは１つの点に限定されるのでしょうか？よく...
猫野の微分積分 三角関数で導関数が解けない関数の極大値を求める問題
問題関数\(f(x)=x+a \cos x (a>1)\)は、0<x<2πにおいて極小値0をとる。このとき、この範囲における極大値を求めよ。解答（解き方）関数のグラフがどのような形になるのかある程度把握しないと、とっつきにくい問題です。y=...
猫野の微分積分 微分を使い増減だけでなく凹凸と±∞での極限値もグラフに書く問題
問題次の関数の増減・極値と凹凸を調べ、グラフをかけ。（１）\(\displaystyle f(x)=\frac{(x-1)^2}{x^2+1}\)（２）\(\displaystyle f(x)=\frac{x}{\log x}\)解答（解き...
猫野の微分積分 ロピタルの定理で極限を求めたら簡単だった事がわかる例題
問題次の極限値を求めるのに、ロピタルの定理をあてはめて確かめてみよ。（１）\(\displaystyle \lim_{x \rightarrow 0} \frac{1-\cos x}{x^2} \)（２）\(\displaystyle \l...