午前午後問題とは
午前午後問題を図で書くと、下記の通りである。
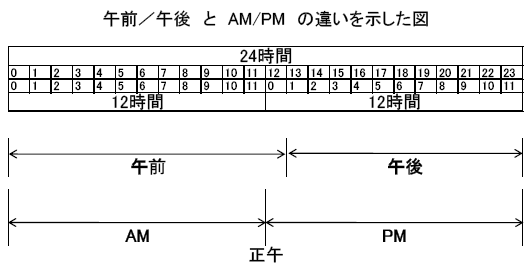
図で示したほうがわかりやすいと思って作図した。
問題は、12時から13時の間を午前というのか、午後というのかであって、話がややこしいことに、午前でも午後でもあるというのが、午前午後問題である。
これは、単に用語の問題であるが、システムで時間計算するときに、面倒を引き起こすのである。たとえば、午前11時半から1時間後と計算すると、12時半となるが、これを午後0時半とせずに、午前12時半と表示せよという仕様があると、単純に12で割った数で時間を計算することができなくなるのである。
したがって、面倒を避けるために、AM/PMで表示するという手段を採用する場合もある。最近は、社会がシステムの都合にすこしずつ寛容になってきて、午前0時半という表示でも、クレームにはならず、むしろ、誤解を避けるために歓迎されてきているようである。
誤解を避けるために、ここではAM/PM用語を採用する。
さて、実は、AM/PM問題には、上記とは別の問題がる。それは、AMとPMの境界の扱いであって、数学では、この境界を含むか含まないかでずいぶんと違った性質がでてくるのである。
さんざん、数直線の開区間、閉区間の例ででてくるのであるが、\((0,1)\)と\([0,1]\)とでは全然位相が異なってしまうのである。
そこで、現実社会として、この境界がどう扱われているのかをここで示したい。
いろんなパターンがあると思うが、代表的な4パターンを例示する。
パターンA

おそらく、これが最も合理的なAM/PMの定義と考える。あくまでも個人的な考えである。
ダブりがないし、開始がはっきりとしている。これは、AM12時などという言い方をせず、PM0時という言い方をするパターンである。
パターンB
これは、ありえないだろう。黒丸の位置を終わりに持ってきたのであるが、なにかと使いにくいはずだ。AM12時から開始して、PM2時までかかった。という風に、0時の代わりに12時を使う。そして、12時を使うために、PMをAMに言い換えたりする。なんだか、AMやPMがいつ始まるのかわからない。
パターンC

これは、苦肉の策のような、さらに混乱をまねくやり方だ。どうしても、正午をAMにしたいがゆえに、ひねり出した。PMを捨ててAM重視のやりかたである。逆に、PM重視の考え方もあるが、数学で区間をこういった場合分けをすることは、まず、ありえないだろう。非対象はシンプルでないがゆえに、美しくない。
パターンD

あろうことか、これが一番現実で使われているようである。
重複を許しているので、時間軸に特別な点の存在を認めてしまってる気がする。
区間の記号であらわすと、
AM=\([0時(0時),12時(12時)]\)
PM=\([0時(12時),12時(24時)]\)
便宜上カッコ内に24時間で時間を表して区別できるように書いた。
AM12時と、PM0時は、同じ時刻を表しているが、AM12時はAMに繋がっていてPMには繋がっていない、また、PM0時はAMにつながっておらず、PMに繋がっている。数学の記号ではこのような状態を表すことができないが、あえて数学的な記号を用いるとすると、半月のように、左半分の黒丸はAM12時で、右半分の黒丸がPM0時といった感じであろう。
同じ時刻に違う名前をあえて付け、正午が(PMの)開始なのか、(AMの)終了なのかのニュアンスを表現できる点で優れていると考えてるのだ。
もちろん、数直線で、半月のような記号を持ち出されても、それがどのような意味を表しているのか、だれも考えてはいない。そのような点の存在は数直線上では許されていない。
まとめ
いろいろ書いたが、結局は誤解がないようにするのが最重要なのであって、そのためには、パターンAの考え方を(少なくとも内部では)しておいたほうがよいと考える。
広告

コメント