第27回(2017年)JMO予選の問題3
黒い部分の面積と白い部分の面積の差を求めよ、こんな問題です。
問題自体は簡単ですが、数値が３桁なので、暗算が得意でなければやる気が失せますね。
私は、失せました。
分配の法則
\((a+b+c)(d+e+f)\\=ad+ae+af+bd+be+bf+cd+ce+cf)\)
分配の法則を図で表すと、
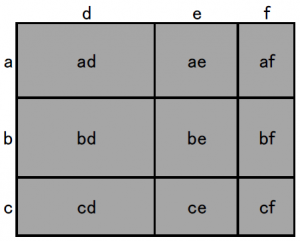
となります。
マス目の面積の総和と大きい長方形の面積が同じという関係式です。
面積は正ですが、分配の法則は負の数でも成立しています。
そこで、辺の長さが負の数の面積もありと思って\(b,e\)の部分の長さが負の場合で分配の法則を作ってみます。
\((a-b+c)(d-e+f)\\=ad-ae+af-bd+be-bf+cd-ce+cf)\)
こんな式になりました。この図を最初の問題とくらべてみてください。
おー、白い部分と負の面積の部分が対応しているではありませんか。
ということで、黒い部分の面積から白い部分の面積を引いた式は、分配の法則の右辺に見事一致しています。
掛け算より足し算の方が計算しやすいので、計算が苦手な私でもなんとか間違えずに計算することができるようになりました。
\((269-292+223)(387-263+176)=200 \cdot 300=60000\)
答え 60000
広告
