足す順番を替えて無限級数の和を求めてみる
下記の二つの例でそれを確かめます。
(1)数列\(\displaystyle a_n=\frac{n+1}{n}-\frac{n+2}{n+1}\)
\(\displaystyle =\frac{1}{n(n+1)}\)
からできる無限級数
\(\displaystyle (\frac{2}{1}-\frac{3}{2})+(\frac{3}{2}-\frac{4}{3})+(\frac{4}{3}-\frac{5}{4})+…\)
\(\displaystyle =\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+…\)
(2)数列\(\displaystyle b_1=\frac{2}{1},b_2=-\frac{3}{2},b_3=\frac{3}{2},b_2=-\frac{4}{3},…\)
からできる無限級数
\(\displaystyle \frac{2}{1}-\frac{3}{2}+\frac{3}{2}-\frac{4}{3}+\frac{4}{3}-\frac{5}{4}+…\)
上記の2つの無限級数の和をそれぞれ求めてみます。
無限級数\(a_1+a_2+a_3+…\)の場合
部分和Snを求めると、
\(\displaystyle S_n\)
\(\displaystyle =(\frac{2}{1}-\frac{3}{2})+(\frac{3}{2}-\frac{4}{3})+…+(\frac{n+1}{n}-\frac{n+2}{n+1})\)
\(\displaystyle =\frac{2}{1}-\frac{n+2}{n+1}\)
\(\displaystyle =\frac{n}{n+1}\)
よって
\(\displaystyle S_n \rightarrow 1 \,( n \rightarrow \infty) \)
となります。収束します。
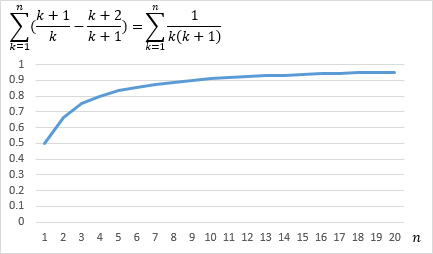
無限級数の和-1に収束していく
無限級数\(b_1+b_2+b_3+…\)の場合
この数列のnが奇数の時のSnを求めると
\(\displaystyle S_n\)
\(\displaystyle =\frac{2}{1}-(\frac{3}{2}-\frac{3}{2})-(\frac{4}{3}-\frac{4}{3})+…+(\frac{n+2}{n+1}-\frac{n+2}{n+1})\)
\(\displaystyle =2\)
となり、
nが偶数の時のSnを求めると
\(\displaystyle S_n\)
\(\displaystyle =(\frac{2}{1}-\frac{3}{2})+(\frac{3}{2}-\frac{4}{3})+…+(\frac{n+1}{n}-\frac{n+2}{n+1})\)
\(\displaystyle =\frac{2}{1}-\frac{n+2}{n+1}\)
\(\displaystyle =\frac{n}{n+1}\)
\(\displaystyle S_n \rightarrow 1 \,( n \rightarrow \infty) \)
となります。
したがって、Snは振動(発散)しています。
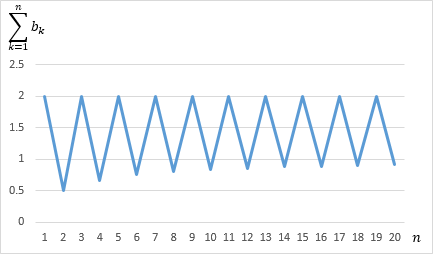
無限級数の和(振動)
数列{bn}による無限級数の和は、奇数項までの部分和は2で、偶数項までの部分和は次第に1に近づくように振動する。
無限級数はカッコによって収束結果が変わる
このように、同じ様にみえる無限級数であっても、カッコがあるとないとで収束・発散が変わってしまうので、無限級数の和は、安易に足す順序を変更してはいけないと言えます。
カッコをつけるというのは、足す順序を変えているともいえます。
数列{bn}を連続する二つの項(2m-1項と2m項)を先に足しておいて、それから無限級数の和をもとめるとそれは、数列{an}の無限級数の和と同じになる。
無限級数の和は、かっこの有り無しで発散したり収束したりします。
カッコの付け方によって、別の値に収束値が変化する場合もあります。
まとめ
- 無限級数の和の式にカッコをつけると収束・発散の結果が変わってしまう。
- カッコの付け方で収束値が変化してしまう場合もある。
- 収束が変化する有名な級数の例
- 1-1+1-1+…+(-1)n+1+… (振動)
- (1-1)+(1-1)+(1-1)+… ⇢ 0(収束)
- 1-(1-1)-(1-1)-… ⇢ 1(収束)



コメント