[msg#wsiki]
問題
次の極限値を求めるのに、ロピタルの定理をあてはめて確かめてみよ。
(1)
\(\displaystyle \lim_{x \rightarrow 0} \frac{1-\cos x}{x^2} \)
(2)
\(\displaystyle \lim_{x \rightarrow 0} \frac{e^x-1-x}{x^2} \)
(3)
\(\displaystyle \lim_{x \rightarrow 0} \frac{e^x-e^{-x}}{\sin x} \)
(4)
\(\displaystyle \lim_{x \rightarrow \infty} \frac{x}{e^x} \)
(5)
\(\displaystyle \lim_{x \rightarrow \infty} \frac{\log x}{x} \)
(6)
\(\displaystyle \lim_{x \rightarrow +0} {x}{ \log x} \)
解答(解き方)
ロピタルの定理には、いろんな前提条件がありますが、初等関数で定義されている関数であれば、前提条件はそれほど気にせずにバンバン使えます。
ただ、求める極限が不定形になっているかどうかは確認する必要があります。
ここだけは、確認します。そうでないと、違った答えが導かれてしまいます。
ロピタルの定理の使い方は簡単です。分母と分子をそれぞれ微分すると不定形が解かれて極限が求めやすくなります。
微分してもまだ不定形が解かれない場合には、再度微分します。
ちなみに、不定形とは、\(\frac{0}{0}\)、\(\frac{\infty}{\infty}\)で表現される極限の式です。
\(0×{\infty}\)や\({\infty}-{\infty}\)のような形も、うまく変形すると\(\frac{\infty}{\infty}\)の形式にできたりします。
(1)
\(\displaystyle \lim_{x \rightarrow 0} \frac{1-\cos x}{x^2} \)
\(\displaystyle =\lim_{x \rightarrow 0} \frac{\sin x}{2x} \)
\(\displaystyle =\lim_{x \rightarrow 0} \frac{\cos x}{2} \)
\(\displaystyle =\frac{1}{2} \)
(2)
\(\displaystyle \lim_{x \rightarrow 0} \frac{e^x-1-x}{x^2} \)
\(\displaystyle =\lim_{x \rightarrow 0} \frac{e^x-1}{2x} \)
\(\displaystyle =\lim_{x \rightarrow 0} \frac{e^x}{2} \)
\(\displaystyle =\frac{1}{2} \)
(3)
\(\displaystyle \lim_{x \rightarrow 0} \frac{e^x-e^{-x}}{\sin x} \)
\(\displaystyle =\lim_{x \rightarrow 0} \frac{e^x+e^{-x}}{\cos x} \)
\(\displaystyle =2 \)
(4)
\(\displaystyle \lim_{x \rightarrow \infty} \frac{x}{e^x} \)
\(\displaystyle \lim_{x \rightarrow \infty} \frac{1}{e^x} \)
\(\displaystyle =0 \)
(5)
\(\displaystyle \lim_{x \rightarrow \infty} \frac{\log x}{x} \)
\(\displaystyle =\lim_{x \rightarrow \infty} \frac{1}{x} \)
\(\displaystyle =0 \)
(6)
無理矢理分数の形に変形します。
変形したあと、不定形になっているのか確認します。
\(\displaystyle \lim_{x \rightarrow +0} {x}{ \log x} \)
\(\displaystyle =\lim_{x \rightarrow +0} \frac{ \log x}{1/x} \)
\(\displaystyle =\lim_{x \rightarrow +0} \frac{ 1/x}{-1/x^2} \)
\(\displaystyle =\lim_{x \rightarrow +0} -x \)
\(\displaystyle =0 \)
どれも、簡単に微分することができますので、ロピタルの定理を使えばいとも簡単に極限が求められます。
答え
(1)
\(\displaystyle \lim_{x \rightarrow 0} \frac{1-\cos x}{x^2} =\frac{1}{2} \)
(2)
\(\displaystyle \lim_{x \rightarrow 0} \frac{e^x-1-x}{x^2} =\frac{1}{2} \)
(3)
\(\displaystyle \lim_{x \rightarrow 0} \frac{e^x-e^{-x}}{\sin x} =2 \)
(4)
\(\displaystyle \lim_{x \rightarrow \infty} \frac{x}{e^x} =0 \)
(5)
\(\displaystyle \lim_{x \rightarrow \infty} \frac{\log x}{x} =0 \)
(6)
\(\displaystyle \lim_{x \rightarrow +0} {x}{ \log x} =0 \)
[ad#foot]
その他の問題: 関数の極限に関する問題 数列の極限の問題一覧 数列の極限に関する問題2
[ad#nekob]
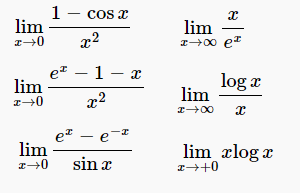




コメント