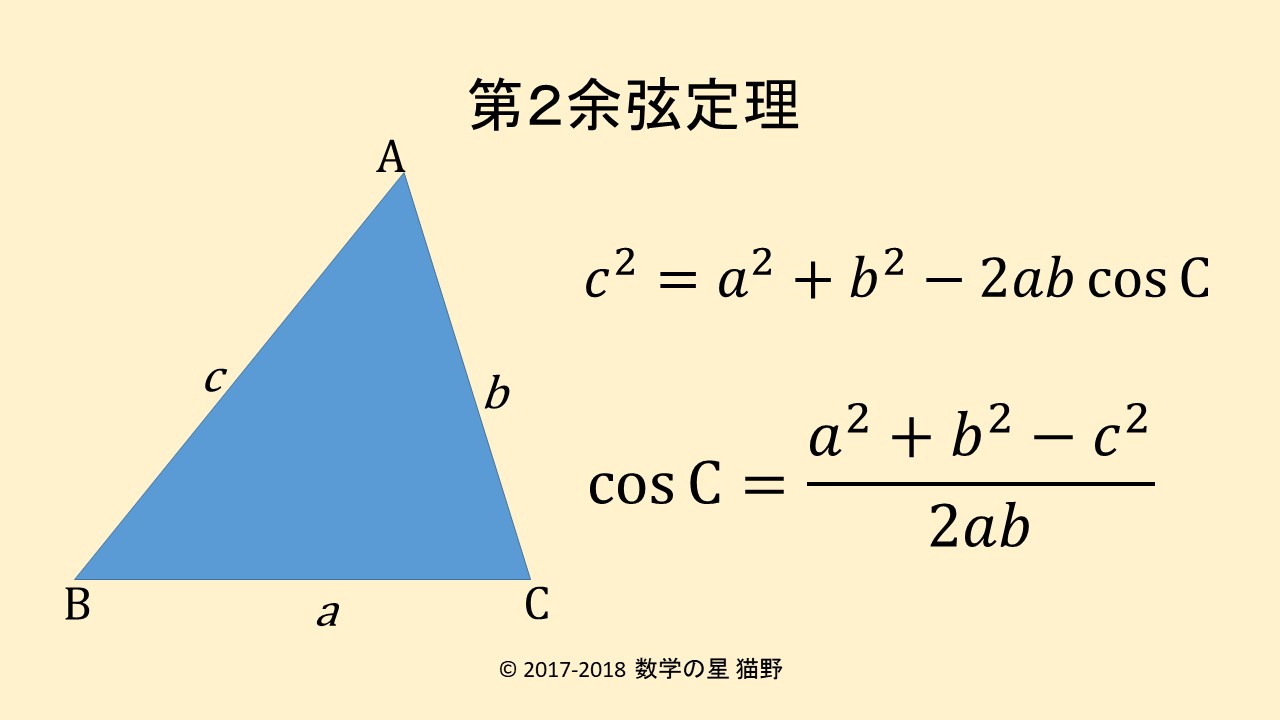
三角形に関する大定理
三角形に関する定理は、山のようにあります。
そのなかでも、辺と角度の関係を表す式はいくつかありますが、
第2余弦定理こそが、それの真骨頂といえます。
この記事は、(第2)余弦定理の覚え方と使い方について書いています。
第2余弦定理
この記事の文字記号の使い方
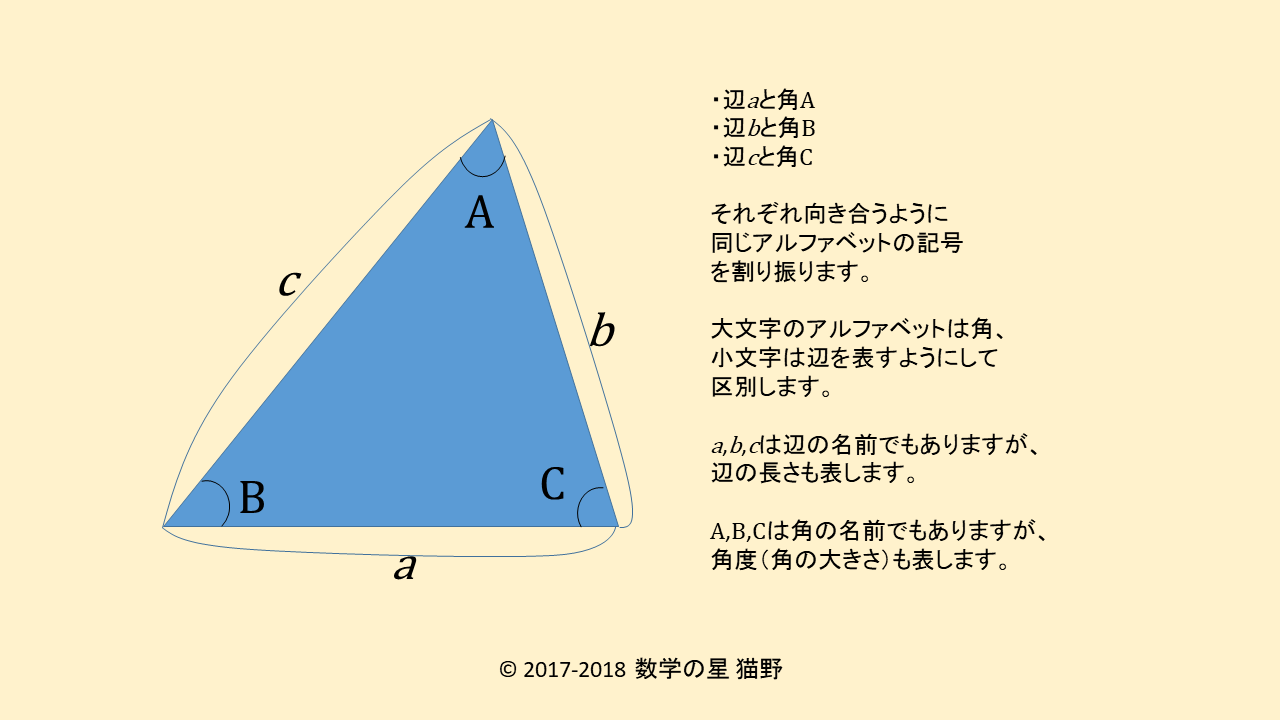
ここでは、ある三角形の三つの辺を
小文字のアルファベトa,b,c
三つの角を大文字のアルファベットA,B,C
で表します。
また、角Aに対応する(向かい合う)辺がaで、
角Bに対応する辺をb、角Cに対応する辺がcと対応するように順番も決めておきます。
さらに、小文字のアルファベットa,b,cは、辺の長さを表す文字としても使います。
同様に、大文字のアルファベットA,B,Cは角の大きさ(単位はラジアン)も表します。
このように、文字(記号)の使い方を決めておくことで、いろいろな記述が勘弁になって便利です。
辺の名前と、辺の長さに同じ文字が使われますが、混乱することはまずありません。
同様に、角に関しても同じことが言えます。
「辺aの長さはaである。」「角Bの角の大きさはBである。」という言い方をしますが、意味は十分に伝わります。
念のために補記しておきますが、
「辺aの長さはaである。」の「辺a」の部分にあるaは、
三角形のある一つの辺を指しており、
「長さはa」の部分の「a」は長さを表す文字式です。
もし、a=5と書いてあった場合は、一つの辺の長さが5であることを表しています。
第2余弦定理とは
第2余弦定理と呼ばれている式は以下の通りです。
\(\displaystyle c^2=a^2+b^2-2ab \cos C \)
\(\displaystyle b^2=c^2+a^2-2ca \cos B \)
\(\displaystyle a^2=b^2+c^2-2bc \cos A \)
注目する角によて、3個の式がありますが、どれも意味は同じですので、一つだけ覚えておけばよいです。
式をみてわかるように、第2余弦定理は、三つの辺の長さと、一つの角の大きさを結びつける式です。
三角形を構成している要素として、三つの辺、三つの角があり合わせて6個の要素がありますが、
第二余弦定理は、このなかの4つの要素を結びつける関係式となっています。
三つの式を書きましたが、代表として各C(または辺c)に基づいた次の式を取り上げます。
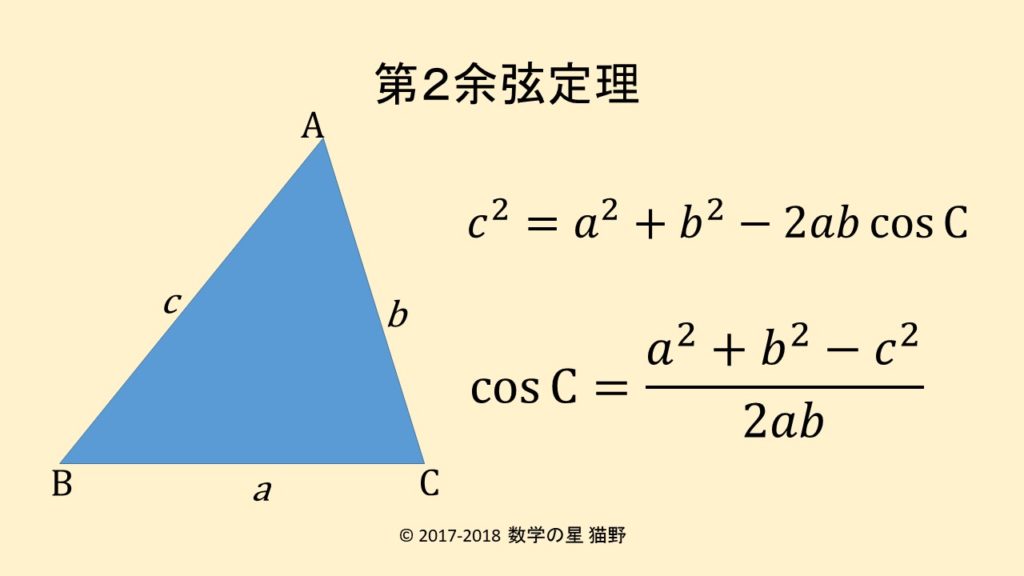
第2余弦定理
\(\displaystyle c^2=a^2+b^2-2ab \cos C \)
これは、角C(もしくはそれに対応する辺c)に注目した式ですが、
変形して、次のように、角Cの部分を強調するために左辺に移した次の形式の式もよく使われます。
\(\displaystyle \cos C = \frac{a^2+b^2-c^2}{2ab} \)
なぜ、第2余弦定理と名付けられて呼ばれているのか
第1余弦定理
第2余弦定理があるということは、第1余弦定理というのもあります。
第1余弦定理
\( \displaystyle c=a \cos B + b \cos A \)
\( \displaystyle b=c \cos A + a \cos B \)
\( \displaystyle a=b \cos C + c \cos B \)
これも、辺と角の関係式ですので、重要といえば重要ですが、実際のところ出番はほとんどありません。
こちらも注目する辺によって3種類の式が挙げられますが、文字が入れ替わっているだけで本質的に表したい内容は1つの式です。
第1余弦定理は、式をよく眺めてみると、3つの辺の長さと、2つの角の大きさに関する関係式になっています。
つまり、三角形の5つの要素に関する関係式です。
第二余弦定理が4つの要素の関係式であったことと比べると、第一の方は一つ要素が多いです。
そのため、第一余弦定理は活躍する出番があまりありません。
繰り返しになりますが、
第一余弦定理では、一つの要素を求めるために、4つの要素を必要とします。
それに対して、第二余弦定理では、一つの要素を求めるために3つの要素で求められます。
したがって、第二余弦定理は第一余弦定理より利点が多いと言えるのです。
ただ、第二余弦定理は二次の式になっています。
対して第一余弦定理は一次の式ですから、第一余弦定理が活躍する場合も稀にあります。
証明も簡単ですから、覚えておいて損はありません。
定理の結果を覚えるよりも、証明の方を覚えたほうが、価値となります。
また、第二余弦定理は第一余弦定理から導くこともできます。
このことから、第二よりも第一のほうは、基本的と考えることができます。
第一、第二という順番も導かれる順番を表していると言えます。
(※注)第2余弦定理をつかって第一余弦定理を証明することもできますが、
第一余弦定理を使ってて第二余弦定理を証明する流れがシンプルです。
余弦定理
cos(コサイン)を使った式で表されているから余弦定理と呼ばれています。
cosは英語のcosineの省略形で、日本語ではコサイン(余弦)と呼ばれる関数です。
単に余弦定理といった場合は、第1余弦定理ではなく、第2余弦定理のことを指します。
三角関数は、その名の通り三角形に関する関数と言えますが、
実は円に関する関数として考えた方がより一般的な性質が見えてきます。
弦とは円弧の直線部分のことですが、
この言葉の意味から考えてcosは、三角関数の一つでありながら実は弦(つまり円)に関する関数であることが暗に見えます。
余弦に対して、正弦という概念もあります。
正弦は、sin(サイン)と書かれます。
余弦定理があるように、正弦定理というのもあります。
正弦定理はsinを含んだ式の定理で、
これも、辺の長さと、角の大きさの間の関係式となっています。
正弦定理も余弦定理にはない特徴があります。
正弦定理は二つの辺と二つの角に関する関係式ですので、
変数の個数としては第二余弦定理と同じです。
正弦定理と余弦ているでお互いをうまく補完しあっており、
両者密接に関係しているので、両者の優劣はつけかねます。
見た目は正弦定理のほうがシンプルに見えるのですが、
ことさら、正弦定理よりも、余弦定理のほうが、活躍の場は多いです。
第2余弦定理のどこが簡潔なのか?
第二余弦定理は、変数が4つあるだけあって、ぱっと見で複雑に見えます。
しかし余弦定理の式は、これ以上簡単には表すことができないぐらいに簡潔な関係式なのです。
そうはいっても長い式なので、丸暗記では細かい部分で間違えてしまう事もあります。
しかし、覚え方で示すように式の構造をよくみると、だんだん、この大定理が辺と角の関係を非常に簡潔な式として表現していることを
実感として認識されるようになります。
辺と角の関係を表すことは、意外にも難しいです。
この定理を三角形をみただけで思いつくひらめきがあるとするなら、
それは驚愕です。
第2余弦定理の覚え方
覚え方は、式を丸呑みするのでなく、三角形の図形をかいて、
式に現れる辺や角がどこの位置にあるのかを確認しながら覚えた方がよいです。
そのほうが、使いやすくもなります。
位置関係が結構対称的になっています。
そして、その位置関係から、どことどこがわかると、どこが求められるという関係も理解していきます。
例えば、「3つの辺の長さがわかっているときには、角Cの大きさを求めることができる。」
これは逆に、「角Cの大きさを求めるためには、3つの辺の長さがわかっていると可能である。」
と言い換えることができます。
「辺cの長さを求めたい場合には、角Cの大きさと、その角を挟む辺の長さがわかればよい。」
こんな感じです。
どこがa,どこがbとか割り当てて覚えるのではなく、
この辺の長さは、残りの辺の長さの自乗と、その挟む角のコサインに辺と辺を掛け合わせて2倍して引く。
といった形で覚えていきます。
この覚え方を文章として読むと、わかりにくいと思いますが、
三角形の位置関係をみながら関係式との対応を把握する事で、
求めたい部分を求めるために、なにが必要かがすぐにわかるようになります。
第二余弦定理はピタゴラスの定理の拡張である
角Cが直角の場合に第二余弦定理がどうなるか必ず確認してください。
直角の余弦はゼロですので、直角三角形に関する第二余弦定理は以下の式になります。
\( \displaystyle c^2=a^2+b^2 -2ab \cos \frac{\pi}{2}\)
\( \displaystyle \cos \frac{\pi}{2}=0\)ですから、
上記の第2余弦定理の式は、直角三角形の場合
\( c^2=a^2+b^2 \)
と簡略化されます。
ピタゴラスの定理(三平方の定理)は直角三角形にしか使えませんでしたが、第二余弦定理は一般の三角形でも使えます。
こうみると、余弦定理の半分はピタゴラスの定理そのものです。
ピタゴラスの定理(三平方の定理)にcosの項を追加したのが第二余弦定理なのです。
これで、余弦定理の半分ぐらいは思い出せるも同然だと思います。
もっとも、ピタゴラスの定理をよく知っているという前提のもとですが。
まあ、これでも、cosの前にある符合がプラスだったか、マイナスだったか、思い出せずによく間違える事もあるので
そこは注意して式としてもしっかり覚えておきましょう。
\( \cos 0 \)、\( \cos \pi \)の場合を考えつくことができれば、
cosの前についている符合も間違えずに決定できるのですが。
ここは、覚えるのに越したことない部分です。
特に、スピード重視で問題を解くときには。
第2余弦定理を使った簡単な例題
一辺が4の長さの正三角形を考えます。
最初に示した記号を使うと、
\( a=b=c=4 \)
\(\displaystyle A=B=C=\frac{\pi}{3}\)
です。
すべての辺の長さと角の大きさはすでにわかっていますが、
余弦定理を使って、「二つの辺の長さとその挟む角」から「残りの辺」の長さを求めてみます。
つまり、\( a,b,C \)から\(c\)を求めてみます。
\(\displaystyle c^2=a^2+b^2-2ab \cos C\)
にそれぞれ\( a,b,C \)を代入すると、
\(\displaystyle c^2=4^2+4^2-2*4*4 \cos \frac{\pi}{3}\)
\(\displaystyle c^2=32-32* \frac{1}{2}\)
\(\displaystyle c^2=16\)
辺の長さcは正の数であることを考慮すると、
\(\displaystyle c=4\)
となって、正しい答えが導き出されました。
また、三つの辺の長さから一つの角の大きさを求めることもできます。
例として、\( a,b,c\)から\(C\)を求めてみます。
先ほど変形した第二余弦定理の式を使ってみます。
\(\displaystyle \cos C= \frac{a^2+b^2-c^2}{2ab}\)
\(\displaystyle \cos C= \frac{4^2+4^2-4^2}{2*4*4}\)
\(\displaystyle \cos C= \frac{16}{32}\)
\(\displaystyle \cos C= \frac{1}{2}\)
これから、Cは\( \frac{\pi}{3} \)
つまり、60度であることがわかります。
一般的には、3つの辺の長さからわかるのは、ある角のコサインです。
コサインの量から角の大きさを求めるためには、計算機による近似計算となります。
第二余弦定理の使い方
第二余弦定理が最もよく使われ、便利に活用されるのは、次の2つのパターンです。
- 三つの辺の長さから角の大きさ(角のコサイン(余弦))を求める場合。
- 二つの辺とその挟む角から、残りの辺の長さを求める場合。
逆に、余弦定理が活用しずらい場合ですが、
- 二つの角と一つの辺から他の辺の長さを求める場合。
この場合は正弦定理の方が役にたちます。
なお、三角形の内角の和は180度という超基本的な第定理がありますから、2つの角の大きさがわかるということは、3つの角の大きさがわかると言う事になります。
角度の計算は非常にややこしいです。角度の代わりに、コサインを使って計算するのですが、それでも計算は辺の長さを主体にしたほうがやり易いです。
計算する上では、できるだけ辺の長さを多く調べた方がより扱い易いです。
問題にもよりますが、
定理(公式)を使う場合、わかっている辺の数に注目するとうまくいくことが多いと思います。
- わかっている辺の数が2または3 ⇨ 余弦定理
- わかっている辺の数が1 ⇨ 正弦定理
- わかっている辺の数が0 ⇨ 個別に考える。