対数の計算方法や公式をいろいろ覚えたけど、
そもそも対数ってどういう概念?
対数について説明せよといわれたら、
まず、指数関数ってのがあって、
それの逆関数が対数関数で、
対数関数で求めた値が対数です。
などといった説明が一般的です。
私も、
このような説明で習いました。
この説明でも、
何度も聞いてれば,
それなりに分かってきますが、
最初は、ただ、
小難しく考えてしまいました。
しかし、
いろいろ勉強してわかったのですが、
対数ってのは、
根本はすごく単純な概念なのです。
まずは、対数の概念を把握しておくと、
数式をつかった対数の説明も
よく意味がつかめてくると思います。
対数の概念は桁数の概念の一般化
ずばり、書きますと、
対数とは桁数のことです!
この事は、
数学やっている人は、
誰でも知っていることではあるのですが、
それを強調して説明している人はあまりみかけません。
恐らく、
対数がわかっている人にとっては
あたりまえのことだからです。
そして、厳密には桁数というと語弊があるからです。
対数を桁数と考えても
概念的には全く問題はないのですが、
用語の使い方が不正確になるため、
いちいち口にださないだけなのです。
心の中では、
対数=桁数
を意識しています。
「対数とは桁数のこと」
\(\displaystyle log_{10}2=0.3010\cdots\)
この例は、
対数を習った時には必ずでてきますね。
対数表にも載っていますが、
この0.3010…という数値がが
一体なにを表しているのか?
これは、
「2の(常用)対数が0.3010…だよ」
ということですが、
砕いて言うと
「数字の2は、桁数が0.3010…の数です」
ということを表す式です。
円周率が3.14…であると覚えたように、
2の常用対数もとりあえず、
暗記しておいても、
やぶさかではありません。
円周率が、
直径1の円の円周の長さを表しているように、
数字2の対数は0.3010は2の(10進数で表した時の)桁数なのです。
つまりある意味で、
「2は、0.3010桁の数である」
と言い換えてもよいということです。
ただ、普通の桁数は自然数です。
小数ではありません。
小数で表された桁数、
それっていったい?
そこがちょっとわかりにくいのですが、
桁数の概念を小数にまで発展すると、
対数の概念に結びつくのです。
2は1桁の整数ですが、
桁数の概念を発展させると、
0.3010…桁の数としてみることができるのです。
対数では、実際の桁数より少し小さな値で表されます。
普通では数字の2は、1桁の自然数ですが、
対数では、0.3010…桁になるというわけです。
桁数とは
そもそも桁数とはなんでしょうか?
桁数とはある数字を書いたときに、
何文字で書くかによってきまります。
たとえば、2桁の数といえば、
10から99の整数がそれに相当します。
数字を2文字つかっているから2桁というわけです。
2桁の例を出しましたが、
1桁の例もだします。
1桁の数といえば、
0から9までの整数です。
ただ、0は特殊な数ですので、
しばらく0の桁数は考えないでください。
0は文字数から言えば1桁ですが、
本当は、文字数が0の空文字で書きたいところを
妥協して1文字で表している事情があるからです。
0の特例があるので、最初に2桁の例をだしました。
0123という数があっても、
これは4桁でなく3桁とみなすじゃないですか。
これと同じです。
0は1桁とみなさないほうが理にかなっているのです。
1桁と2桁の境界がどこにあるのかというと、
9と10です。
9が一桁で、10が2桁。
2桁と3桁の境界は、
99と100の間です。
当たり前のことですが、
数が大きくなると桁数も大きくなっていきますね。
1から9が1桁
10から99が2桁
100から999が3桁
・・・
数が大きくなると桁数も大きくなる、
逆に、桁数が大きくなると数も大きくなります。
ただ、1と9とでは9が大きいのですが、
どちらも桁数としては1で同じ桁数です。
ここで、桁数は整数(自然数)なので、
飛び飛びになってしまいますが、
小数を使えば、
連続的にできるじゃないですか。
これが対数です。
小数を使った桁数が対数というわけです。
ただ、桁数と対数は、
ちょっとずれがあります。
ここがちょっとややこしいのですが、
どういうことかといいますと、
10の(常用)対数は1なのです。
10は2桁ですが、対数としては1です。
1少なくなるのですね。
関係としては、
対数を切り捨てして1を加えると桁数になります。
|
数 |
常用対数 \(\log(n)\) |
\(\log(n)\) の切り捨て |
\(n\)の 桁数 |
| 1 | 0 | 0 | 1 |
| 2 | 0.3010 | 0 | 1 |
| 3 | 0.4771 | 0 | 1 |
| 4 | 0.6021 | 0 | 1 |
| 5 | 0.6990 | 0 | 1 |
| 6 | 0.7782 | 0 | 1 |
| 7 | 0.8451 | 0 | 1 |
| 8 | 0.9031 | 0 | 1 |
| 9 | 0.9542 | 0 | 1 |
| 10 | 1 | 1 | 2 |
剰余対数\(\log(n)\)とは、\(n\)の常用対数(近似値)で、それを切り捨てした値を切り捨て列にあらわしています。
念のために書いておきますが、対数は一般的に無限小数です。
ここでは、小数第4位まで書いておきました。
ところで、同じ数でも10進数と2進数では桁数が異なります。
例えば、5は十進数では1桁ですが、2進数では\((101)_2\)となりますから3桁です。
このように、桁数を考える場合、基数がなんであるか(何進数であるか)を決めて置かなければなりません。
対数では、その数のことを「底」と呼びます。
いままでは、暗黙に10進数で考えていましたので底は10でありました。
そして、なにげに「対数」のことを「常用対数」と書いていました。
対数は10を底にしている場合には、特別に常用対数と呼びます。
逆に、常用対数といえば、底を10で考えているということです。
|
数 |
底が2の 対数 \(\log_2(n)\) |
\(\log_2(n)\)の 切り捨て |
2進数での桁数 |
| 1 | 0 | 0 | 1 |
| 2 | 1 | 1 | 2 |
| 3 | 1.5850 | 1 | 2 |
| 4 | 2 | 2 | 3 |
| 5 | 2.3219 | 2 | 3 |
| 6 | 2.5850 | 2 | 3 |
| 7 | 2.8074 | 2 | 3 |
| 8 | 3 | 3 | 4 |
| 9 | 3.1699 | 3 | 4 |
| 10 | 3.3219 | 3 | 4 |
2進数の場合も、2を底とした対数の整数部分に1を加えたのが桁数になっていますね。
対数は、桁数を小数を使ってより精度良く表した数とも言えます。
当然ながら、対数がわかれば桁数もわかります。
例えば、1万が2進数で何桁なのかは、2を底とした10000の対数が計算できればよいのです。
対数の記号\(log\)を使って書くと、
\(\log_2(10000)\)が計算できれば、2進数での桁数がわかります。
対数表や計算機で計算すると、
\(\log_2(10000)=13.2877…\)
であることがわかります。
13.2877は切り捨てして1を足すと14ですから、
10000は2進数で表すと、14桁の数となります。
桁数と対数のグラフ
このグラフをみてください。
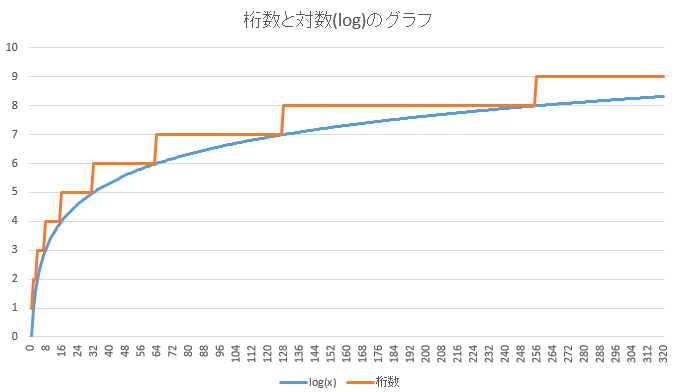
桁数を表している関数がオレンジの線です。
水色の線が対数(log関数)のです。
桁数を表す関数は階段状になっていますが、
その角を削った形が対数のグラフになっています。
このグラフから、
対数は桁数と密接に関係していることが
わかります。
なお、念のために注意点を書いておきますが、
このグラフはわかりやすいよう
2進数で表した時の桁数の場合でかいています。
すなわち底は2の場合のグラフです。
底が10の場合は、
もっと傾斜がゆるやかなグラフとなり、
相当に横長のグラフにしないと、
階段状の部分があまりでてこないため、
階段状の部分が多くでてくるように桁数は2進数に変換した場合にしてあるのです。
対数のいいところ
対数のいいところは、
本当にいろいろありますが、
その根幹として、
(1)大きい数を小さい数で表すことができる。
(2)掛け算が足し算になる。
(3)対数から元の数がわかる
この3点を挙げることができます。
(1)については、日常的に最も実用的に使われています。
100万円以上の収入の事を7桁収入、
1000万円以上の収入を8桁収入ということがあります。
ある程度大きな数を伝える場合には、桁数で言ったほうがイメージが付きやすいし、比較しやすいのです。
(2)についてはこういうことです。
2桁の数と3桁の数をかけると5桁の数になります。
これと同じことが対数でも言えます。
対数の場合は正確です。
ですから掛け算で表される大きな数が何桁なのか、
かけている数の対数を足していけば計算できます。
よくある問題は、2の100乗が何桁かという問題ですね。
2を100個かけるということは、
対数でいうと
\(\displaystyle log(2)\)を100個足すということですから、
\(\displaystyle log_{10}2=0.3010\)がわかっているとすると、
\(\displaystyle log_{10}(2^100)=30.10\)
となって、
2の100乗は31桁(10進数)の数であることがわかります。
(3)については、桁数にない利点でもあります。
桁数の場合、2桁の整数というと、10から99までの90個が該当します。
逆にいうと、それら90個の数をまとめて2桁の数と呼んでいるわけです。
対数の場合は、これが1つになります。
つまり、(常用対数で)0.3010…の桁数の数は、2だけになります。
0.3010…と無限小数なので小数点以下をすべて書きあわわすことはできませんが、
一対一で対応します。
しかも、対数は整数だけでなく、実数に対してもあります。
例えば、2.5が何桁かといわれると、普通は答えに窮すると思います。
桁数の定義がはっきりしていないともいえますが、
「1桁」とも言えれば「2桁」とも、はたまた「桁数はない」と答える人もいるかもしれません。
考え方、解釈の仕方で答えが揺れてしまいますが、対数の場合は、一つの実数に対応してきます。
ちなみに、2.5の常用対数は、0.39794…です。
それは、無限小数で、
2の常用対数(0.3010…)と
3の常用対数(0.4771…)の
間にある数となっています。
これは余談ですが、
対数から桁数に変換する公式、
「切り捨てて1を加える」で考えると、
0.39794…は、小数点以下を切り捨てして0,
それに1を加えると1になりますから、
2.5は1桁であると考えることもできます(そういう解釈もできます)。
対数のさらなる理解へ
対数について、
その発想の原点、
根本となる概念を
説明してきました。
ただ、概念だけを掴んだだけでは
応用が効きません。
対数を桁数で把握するのは、
数の神秘にせまる突破口ではありますが、
まだまだ序の口、入り口に踏み込んだだけに過ぎません。
実は、この奥にもっと深淵なる数の世界が広がっています。
そこに至るために、
少なくとも、
ネイピア数、
自然対数、
指数関数、
などの関連性を把握していく必要があります。
対数を単なる桁数の一般化としてみるのは、
非常にもったいない話です。
対数を表す\(\displaystyle log\)の記号を使うと、
いろいろ便利な計算ができ、
さらに対数が取り扱いやすくなります。


