複素数でも使える拡張不等式で複素数の範囲で不等式を解いてみます。
ここでは、複素数体\(\mathbb{C}\)のポジティブ集合\(P\)を下記のように定義します。
\(P:=\{x+yi | x>0 \: \lor \: (x=0, y>0) 、\: x, y \in \mathbb{R} \} \)
すなわち、複素平面の右半分と、虚軸の上半分になります。
拡張不等式は、
\[\displaystyle α<_θ β \Rightarrow \frac{β-α}{θ} \in P\]と解釈されます。
問題1 \(0<_1 z\)
\(z=x+yi, x,y \in \mathbb{R}\)とする。
\(\displaystyle 0<_1 z\)
\(\displaystyle \Rightarrow \frac{(x+iy)-0}{1} \in P\)
\(\Rightarrow x+yi \in P\)
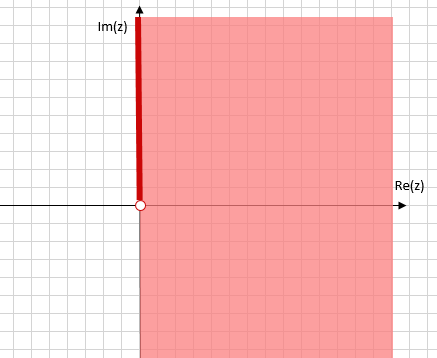
\(0<_1 z\)となる\(z\)は、ポジティブ集合\(P\)全体となります。
問題2 一次不等式 \(5+2i<_1 z\)
\(z=x+yi, x,y \in \mathbb{R}\)とする。
\(\displaystyle 5+2i<_1 z\)
\(\displaystyle \Rightarrow \frac{(x+yi)-(5+2i)}{1} \in P\)
\(\Rightarrow (x-5)+(y-2)i \in P\)
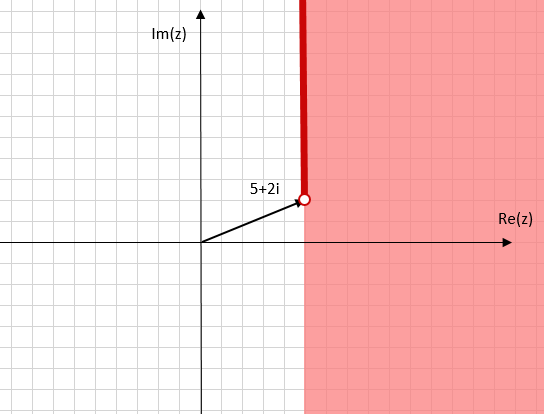
解は次の二つの領域の結合となります。
(1) x-5>0
(2) x-5=0,y-2>0
問題3 一次不等式 \(5+2i<_i z\)
向きが\(i\)の一次不等式の問題です。
\(z=x+yi, x,y \in \mathbb{R}\)とする。
\(\displaystyle 5+2i<_i z \)
\(\displaystyle \Rightarrow \frac{(x+yi)-(5+2i)}{i} \in P\)
\(\Rightarrow (y-2)+(-x+5)i \in P\)
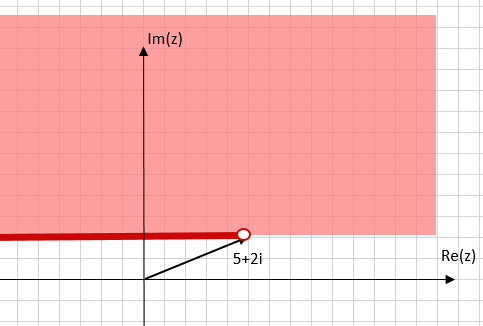
解は次の二つの領域の結合となります。
(1) y-2>0
(2) y-2=0,-x+5>0
問題4 一次不等式 \(5+2i<_{[1-i]} z\)
向きが\(1-i\)の一次不等式の問題です。
\(z=x+yi, x,y \in \mathbb{R}\)とすると、
\(\displaystyle 5+2i<_{[1-i]} z \)
\(\displaystyle \Rightarrow \frac{(x+yi)-(5+2i)}{1-i} \in P\)
\(\displaystyle \Rightarrow \frac{(x-y-3)+(x+y-7)i}{2} \in P\)
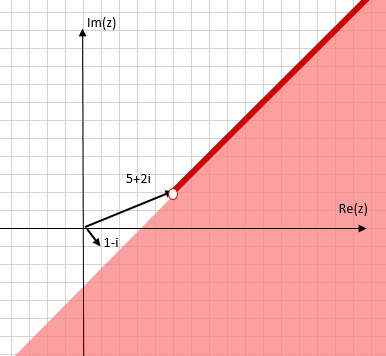
解は次の二つの領域の結合となります。
(1) x-y-3>0
(2) x-y-3=0,x+y-7>0
まとめ
一次拡張不等式の解は、複素平面を2分する直線で仕切られた領域となります。


