三角形の辺の長さなどから角度(角の大きさ)を求める方法です。
次の2パターンに分けて説明します。
- パターン1:3辺の長さから角度を求める方法
- パターン2:2辺の長さと1つの角度から残りの角の大きさを求める方法
メインで活躍する公式は第二余弦定理です。
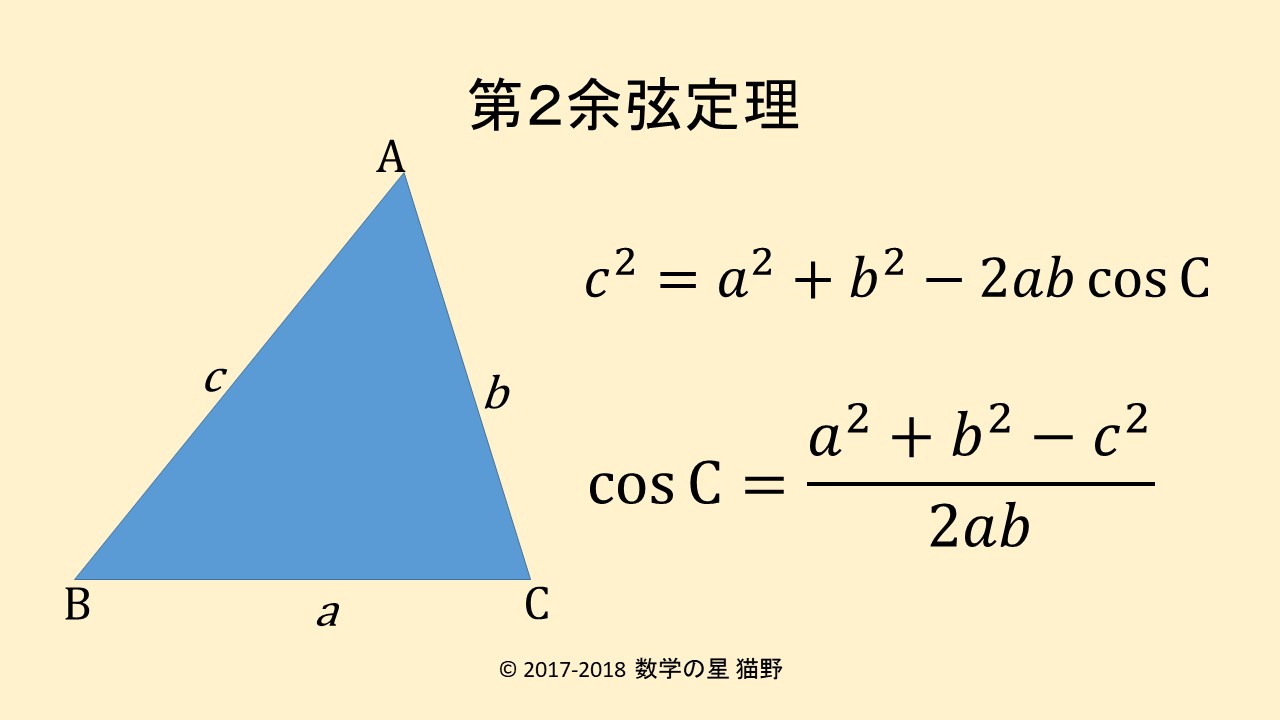
(第2)余弦定理
\(\displaystyle a^2=b^2+c^2-2bc \, \cos A \)
\(\displaystyle b^2=c^2+a^2-2ca \, \cos B \)
\(\displaystyle c^2=a^2+b^2-2ab \, \cos C \)
ものすごく強力な公式です。
第二余弦定理については知っているという前提で問題を解いていきます。
同じ第2余弦定理ですが、角度(正確には角の余弦)を求めるために、
以下のように変形した形もあります。
(第2)余弦定理変形版
\(\displaystyle \cos A=\frac{b^2+c^2-a^2}{2bc}\)
\(\displaystyle \cos B=\frac{c^2+a^2-b^2}{2ca}\)
\(\displaystyle \cos C=\frac{a^2+b^2-c^2}{2ab}\)
三角形の3辺の長さから角度を求める

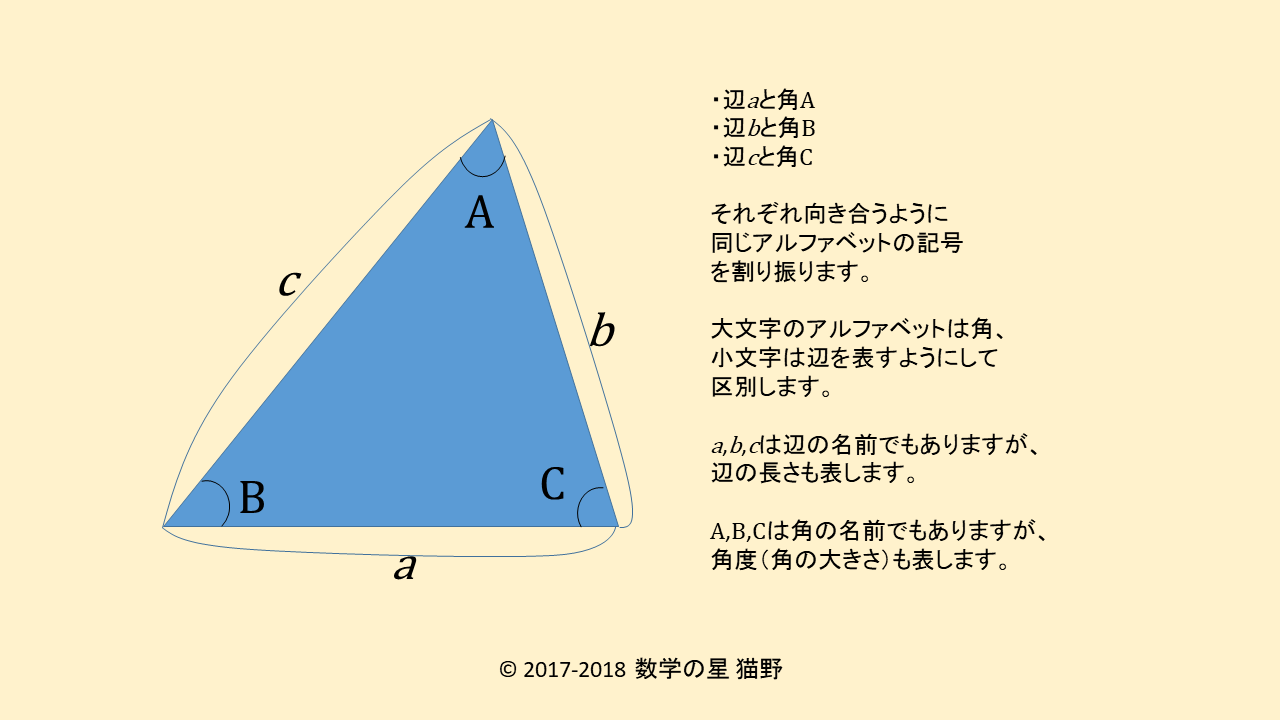
三角形の記号
使用する記号ですが、図のように、三辺の長さを\( a,b,c \)、角度を\(A,B,C\)で表すことにします。
角度は、次の2段階のステップで求めます。
- 求める角度の余弦(cos(コサイン))を求める。
- 余弦から角度を求める。
第1ステップで余弦定理を使います。
余弦定理の公式を覚えていればそれに当てはめるだけで余弦が求まります。
辺から余弦(コサイン)を求める
第二余弦定理を変形した公式を使えば、辺の長さから余弦を求めることができます。
第二余弦定理の使用例
辺の長さが、それぞれ4,5,6であるような三角形を考えます。
この三角形の余弦つまりコサインをそれぞれ余弦定理を使って求めます。
ここでは、便宜上、\(\displaystyle a=4,b=5,c=6\)と\( a,b,c \)を割り当てますが、
\(\displaystyle a=5,b=3,c=6\)としても問題ありません。
ただ、aとA、bとB、cとCが向き合うように決める必要があります。
さて、具体的に角Aの余弦、つまり\(\cos A\)を求めてみます。
公式の使い方ですが、実は頭の中では次のように考えて使います。
求めたい角度の対辺はどれか?
求めたい角度を挟んでいる辺はどれか?
もし、求めたい角がAであるのなら、
対辺はa、
角Aを挟んでいる辺はbとc
となります。
角を挟む辺は2つありますが、それをそれぞれ(挟む辺1)、(挟む辺2)とかくと
余弦定理は次のような公式になります。
余弦定理
\(\displaystyle \cos (求めたい角)=\frac{(挟む辺1)^2+(挟む辺2)^2-(対辺)^2}{2×(挟む辺1)×(挟む辺2)}\)
\(\displaystyle a=4,b=5,c=6\)の場合、
角Aの余弦は、対辺=4,挟む辺1=5、挟む辺2=6
となりますから、
\(\displaystyle \cos A=\frac{5^2+6^2-4^2}{2×5×6}\)
\(\displaystyle =\frac{25+36-16}{60}\)
\(\displaystyle =\frac{45}{60}\)
\(\displaystyle =\frac{3}{4}\)
となります。
挟む辺を入れ替えて、
対辺=4,挟む辺1=6、挟む辺2=5としても
同じ結果になることに注目しておきましょう。
同じように、角Bに対しても、対辺、挟む辺をみつけて\( \cos B\)を求めてみます。
対辺=5,挟む辺1=4、挟む辺2=6として
\(\displaystyle \cos B=\frac{4^2+6^2-5^2}{2×4×6}\)
\(\displaystyle =\frac{16+36-25}{48}\)
\(\displaystyle =\frac{27}{48}\)
\(\displaystyle =\frac{9}{16}\)
角Cの場合は、
対辺=6,挟む辺1=4、挟む辺2=5として
\(\displaystyle \cos C=\frac{4^2+5^2-6^2}{2×4×5}\)
\(\displaystyle =\frac{16+25-36}{40}\)
\(\displaystyle =\frac{5}{40}\)
\(\displaystyle =\frac{1}{8}\)
となって、それぞれの角の余弦(コサイン)が求められます。
余弦(コサイン)から角度を求める
実は、一般的に余弦から角度を求めるには計算機による近似計算になります。
先に書いた三辺の例の角度を計算すると、
\(\displaystyle \cos A=\frac{3}{4}\)
\(\displaystyle \cos B=\frac{9}{16}\)
\(\displaystyle \cos C=\frac{1}{8}\)
からそれぞれの角度を計算機で求めると
\(\displaystyle A=0.723=41.4°\)
\(\displaystyle B=0.973=55.8°\)
\(\displaystyle B= 1.445=82.8°\)
となります。
等式で書いていますが、これは近似式で求めた値です(誤差を含んでいます)。
このように、一般的に角度は近似値で求めることになります。
ただ、正確な角度がわかる例もいくつかあります。
その中でも角度がわかる、特に特別な(余弦)値は、マイナスも含めて書くと
\(\displaystyle 0,\frac{1}{2}, \frac{\sqrt{2}}{2}, \frac{\sqrt{3}}{2}, 1\)
\(\displaystyle -\frac{1}{2}, -\frac{\sqrt{2}}{2}, -\frac{\sqrt{3}}{2}, -1\)
です。
余弦(コサイン)がこれらの値の場合に対応する角度は次の通りです。
これらは、最もよく使われる余弦と角度の対応表ですから、確実に覚えておく必要があります。
|
余弦 \( \cos \theta \) |
\(\displaystyle 0\) | \(\displaystyle \frac{1}{2}\) | \(\displaystyle \frac{\sqrt{2}}{2}\) | \(\displaystyle \frac{\sqrt{3}}{2}\) | \(\displaystyle 1\) |
|
角度 \( \theta \)単位(ラジアン) |
\(\displaystyle \frac{\pi}{2}\) | \(\displaystyle \frac{\pi}{3}\) | \(\displaystyle \frac{\pi}{4}\) | \(\displaystyle \frac{\pi}{6}\) | 0 |
|
角度 \( \theta \)単位(度) |
90° | 60° | 45° | 30° | 0° |
余弦(コサイン)がマイナスの場合の角度は、90度より大きくなります。
|
余弦 \( \cos \theta \) |
\(\displaystyle -\frac{1}{2}\) | \(\displaystyle -\frac{\sqrt{2}}{2}\) | \(\displaystyle -\frac{\sqrt{3}}{2}\) | \(\displaystyle -1\) |
|
角度 \( \theta \)単位(ラジアン) |
\(\displaystyle \frac{2\pi}{3}\) | \(\displaystyle \frac{3\pi}{4}\) | \(\displaystyle \frac{7\pi}{6}\) | \(\displaystyle \pi\) |
|
角度 \( \theta \)単位(度) |
120° | 135° | 150° | 180° |
角度を求める問題では、このような特別な計算値がでることが多いので、
求める角度が45度であったり60度である事が多いです。
一言テクニック
辺の長さから角度を求める問題では、答えが15°の倍数になっている可能性が非常に高いわけです。
なかでも、答えが60°である可能性は極めて高いといえます。
感で答えを求めるとなると、ラフな図をかいて、30°,45°,60°,90°のどれに近いか見極める方法がかなり有効です。
計算せずとも答えにたどり着くことができます。
三角形の2辺と一つの角度から他の角の大きさを求める
これは、「パターン1:三角形の3辺の長さから角度を求める」の応用で求めることができます。
まず、余弦定理を使って、長さが不明である辺の長さを求めます。
すると、3辺の長さがわかるので、残りの角度も計算できます。