[msg#wsiki]
数列の極限に関する問題です。
解き方や解答はそれぞれの解答ページを参照してください。
1.数列の極限を求める問題と解き方cosn(a)/(1+sinn(a))他
問題1
\(\displaystyle \frac{\cos^n \alpha}{1+\sin^n \alpha}\)
の極限をもとめよ。
問題2
\(\displaystyle \frac{1}{n^3}(1^2+2^2+\cdots +n^2)\)
の極限をもとめよ。
問題3
\(\displaystyle \frac{1}{n}(\frac{3n}{n}+\frac{3n+1}{n}+\cdots +\frac{4n-1}{n})\)
の極限をもとめよ。
問題4
\(\displaystyle \frac{1 \cdot 2 + 2 \cdot 3 + \cdots +n \cdot (n+1) }{n^3}\)
の極限をもとめよ。
2.はさみちで求める数列の極限の問題「n(1/n)の極限を求めよ」
問題1
(1)\(\displaystyle 1+\frac{1 }{\sqrt{n}} \gt \sqrt[2n]{n}\) (n=1,2,3,…)を証明せよ。
(2)\(\displaystyle \lim_{n \rightarrow \infty}{\sqrt[n]{n}}\) をもとめよ。
3.名古屋大学-数列の極限を求める問題の解き方
問題1
aは正の数、p,qはp>qの正の整数、
\(a_1=1、a_n^p a_{n-1}^q=a \)(n≧2)
をみたす正数列を{an}とする。このとき、
\(\displaystyle \lim_{n\rightarrow \infty} a_n\)を求めよ。
4.漸化式数列の極限問題と解き方(階差数列あり)3問
問題1
次の漸化式から\(\displaystyle \lim_{n\rightarrow \infty} a_n\)を求めよ。
\(a_1=0,a_2=1,a_{n+2}=(1+k)a_{n+1}-ka_n\)
問題2
次の漸化式から\(\displaystyle \lim_{n\rightarrow \infty} a_n\)を求めよ。
\(a_1=1,3a_{n+1}=a_n-2^n\)
問題3
次の漸化式から\(\displaystyle \lim_{n\rightarrow \infty} a_n\)を求めよ。
\(\displaystyle a_1=1,a_{n+1}=\frac{a_n}{2a_n+3}\)
5.漸化式を等比数列に変形して解く数列の極限問題
問題1
数列\(\{a_n\}\)において、\(a_n=\sqrt{3 a_{n-1}+10} \; (n \ge 2) \; a_1 \ge 0\)のとき、
(1)\(\displaystyle |a_n-5| \le \frac{3}{5}|a_{n-1}-5|\; (n \ge 2 ) \)を証明せよ。
(2)\(\displaystyle \lim_{n \rightarrow \infty} a_n\)を求めよ。
6.東京女子大学ー数列の極限を求める問題と解き方
問題1
\(\displaystyle a_1=2,\;a_{n+1}=\frac{1}{a_n}+\frac{a_n}{2}\; (n=1,2,\cdots)\)
のとき、数列\(\{a_n\}\)は極限\(\sqrt{2}\)をもつことを示せ。
7.早稲田大学教育ー数列の極限を求める問題
問題1
\(\displaystyle f(x)=x+\frac{1}{2}-\frac{1}{2}|x-1|\)とする。
xを実数とし、\(x_1=f(x),x_2=f(x_1),\cdots,x_n=f(x_{n-1})\)
とするとき、数列\(\{x_n\}\)が収束するようなxの範囲とそのときの\(\displaystyle \lim_{x \rightarrow \infty} x_n\)を求めよ。
8.広島大学ー数列の極限を求める問題と解き方
問題1
行列
\(\displaystyle A = \left(
\begin{array}{cc}
a & b \\
1-a & 1-b
\end{array}
\right)
\)
のn個の積\(\displaystyle A^n\)は、
\(\displaystyle \left(
\begin{array}{cc}
a_n & b_n \\
1-a_n & 1-b_n
\end{array}
\right)
\)
の形になる。
ただし、\(b \ne 0、a-b \ne -1\)とする。
(1)
\(\displaystyle a_n, b_nをa,b,c\)で表わせ。
(2)
\(\displaystyle \lim_{n \rightarrow \infty} \frac{a_n}{b_n}\)
を求めよ。
(広島大)
9.正三角形の辺上の点から垂線を下ろし続けた先の点
問題1
正三角形ABCの辺AB上の1店をP1とする。P1から辺BCへ下ろした垂線の足をQ1、Q1から辺CAに下ろした垂線の足をR1、R1から辺ABへ下ろした垂線の足をP2として、P2からさらに同じ操作を繰り返してQ2、R2、P3、Q3、R3、…とする。
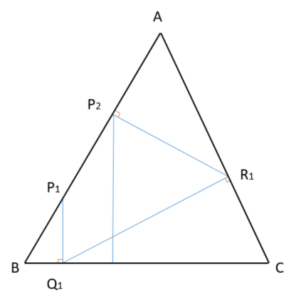
n→∞のとき、Pnはどの点に近づくか。
10.三角形の底辺を等分した長さに関する極限
問題1
三角形ABCにおいてBC=a,CA=b,AB=cとする。
BCをn等分する点をP1,P2,…,Pn-1としPn=Cとする
このとき、
\( \displaystyle \lim_{n \rightarrow \infty} \frac{1}{n}(AP_1^2+AP_2^2+\cdots+AP_n^2) \)
を求め、これをa,b,cで表わせ。
[ad#foot]
その他の微分積分に関する問題
[ad#nekob]
