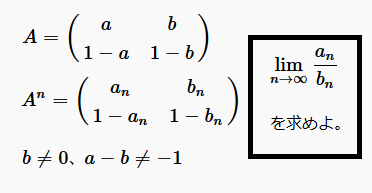 猫野の微分積分
猫野の微分積分 広島大学ー数列の極限を求める問題と解き方
問題行列\(\displaystyle A = \left(\begin{array}{cc}a & b \\1-a & 1-b\end{array}\right)\)のn個の積\(\displaystyle A^n\)は、\(\displ...
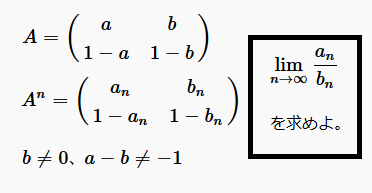 猫野の微分積分
猫野の微分積分 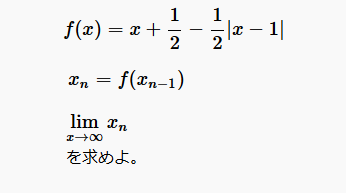 猫野の微分積分
猫野の微分積分 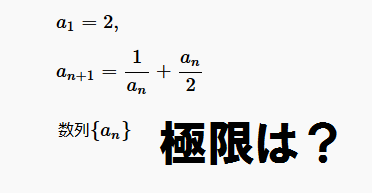 猫野の微分積分
猫野の微分積分 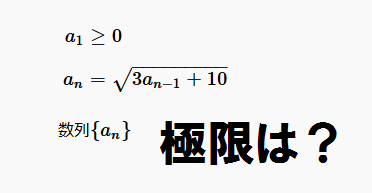 猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分 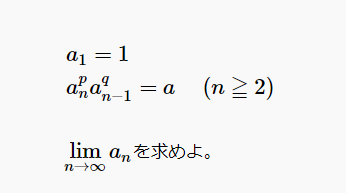 猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分 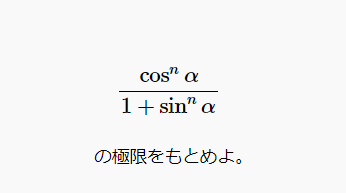 猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分