サンダラムの篩を使った方法はこちらにあります。
素数の判定
なにか与えられた自然数が素数かどうか判定するには、その数の約数を調べればわかります。
約数を調べるためには、その数以下の自然数で割ってみて、割り切れているかどうかで調べます。
例えば、53が素数かどうか調べるためには、53を2、3、4、5、・・・、52まで割り切れるかどうかを調べることになります。
もし、この中に一個でも約数があれば、それは素数ではありません。合成数となります。
これが基本的な素数の判定方法です。
ただ、この方法は、かなり効率が悪く、改善の余地があります。
まず、割り切れるかどうかを調べる数ですが、もし約数があったとすると、その約数の一つは必ず、\sqrt{53}以下になっているはずです。したがって、割る数は\sqrt{53}以下で調べればよいことになります。
7 \lt \sqrt{53} \lt 8なので、53の場合は、2,3,4,5,6,7で割り切れるかどうかを調べればよいことになります。
さらに、2,3,4,5,6,7のうち、4や6は割り切れるか調べる必要はありません。例えば、4で割り切れたとしたら、それは2でも割り切れるはずで、2で割り切れるかどうかを試しているのであれば、4は試す必要がないです。つまり、7以下の素数だけで割り切れるかどうかを調べればよいことになります。
ですから、まとめると、素数かどうか判定するためには、その素数の平方根以下の素数で割り切れるかどうかを調べれば判定できることになります。
これが素数判定の基本です。素数判定のプログラムを作る場合には専らこの方法が使われます。
ただ、上記の方法を使うにしても、素数判定するために、素数リストが必要です。7以下の素数は、2,3,5,7とすぐにわかりますが、数値が大きくなってくると、簡単にはわかりません。
たとえば、100までの素数リストを作るためには、100以下の自然数が素数かどうかを判定していけばできます。
100程度の小さな数では、コンピュータを使わなくても、暗算で素数リストを作ることも可能でしょうが、数値が大きくなればなるほど素数リストを作るのは大変な作業となります。150桁の数になってくると、コンピュピュータでもそう簡単に素数判定はできません。
素数リストがあると便利です。すぐに素数かどうか判定できるからです。素数リストを効率よく作成する方法として、エラトステネスの篩をつかった方法があります。
エラトステネスの篩(ふるい)
それでは、エラトステネスの篩をつかって100以下の素数リストを求めてみます。
まず、1は素数ではないので、除外し2から100までのリストをつくります。
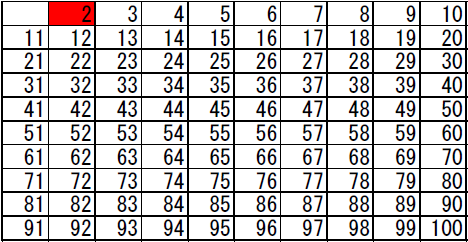
このリスト(表)から、合成数を消していくのがエラトステネスの篩です。
まず、小さい数字で塗りつぶされていない数を探します。上の表では2がそれに該当します。これで2は素数確定です。目印として赤く塗っています。
そして、(2を除く)2の倍数を塗りつぶします。黄色で塗りつぶしたのが下記の表です。
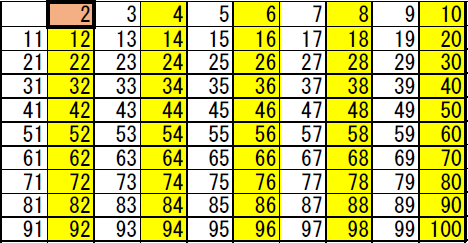
次に、まだ塗りつぶされていない数を小さいほうから検索します。3が該当しますので、赤で塗りつぶしました。この3は素数確定です。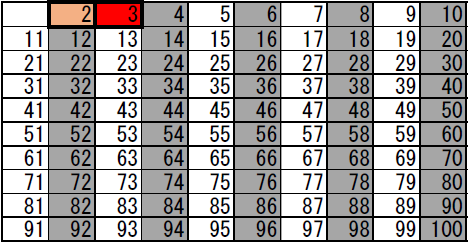
(3はそのままにしておいて)3の倍数を塗りつぶします。すでに2の倍数で塗りつぶされていたところもありますが、わかりやすく黄色で再度塗りつぶしました。それが下記の表です。
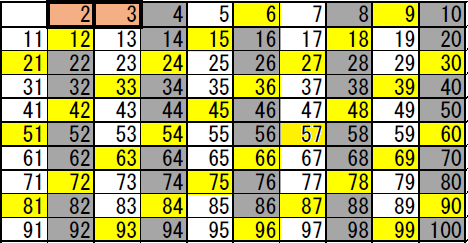
塗りつぶしたら、小さい方から塗りつぶされていない数を探します。4はすでに塗りつぶされていますので、5がそれに該当します。同様うに、5を除く5の倍数を塗りつぶします。
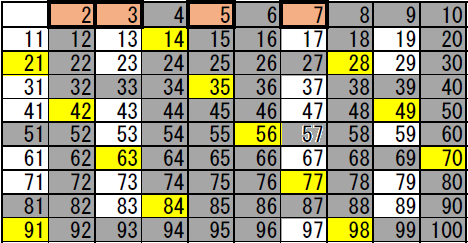
さらに、塗りつぶされていない数を探します。7ですから、その倍数を塗りつぶします。

これで、100までの自然数で2,3,5,7の倍数が塗りつぶされました。
次の素数は11になりますが、10×10=100なので、100までの素数を求める場合は、10以下の素数の塗りつぶしで完了します。上の表をみると、10まで全て塗りつぶされていることがわかりますので、これで作業完了です。
上の表で塗りつぶされずに残った数が素数となります。
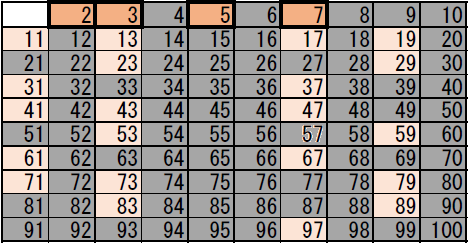
この表から、100以下の素数が判明します。
素数リスト「2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97」のできあがりです。
エラトステネスの篩で効率よく素数リストを作成することができました。
まとめ
- 素数かどうか判定するためには、約数を調べる。
- 約数は平方根以下の数まで調べれば良い。
- 素数リストを作成するにはエラトステネスの篩が有効。
[ad#foot]
