数直線全体をぎゅ~っと縮めて開区間(-1,1)に対応させる
下記に実数直線を開区間(-1,1)に埋め込んだ状況を図で示します。
いろんな関数を使う方法が考えられますが、できるだけ単純な関数を選んで埋め込みました。
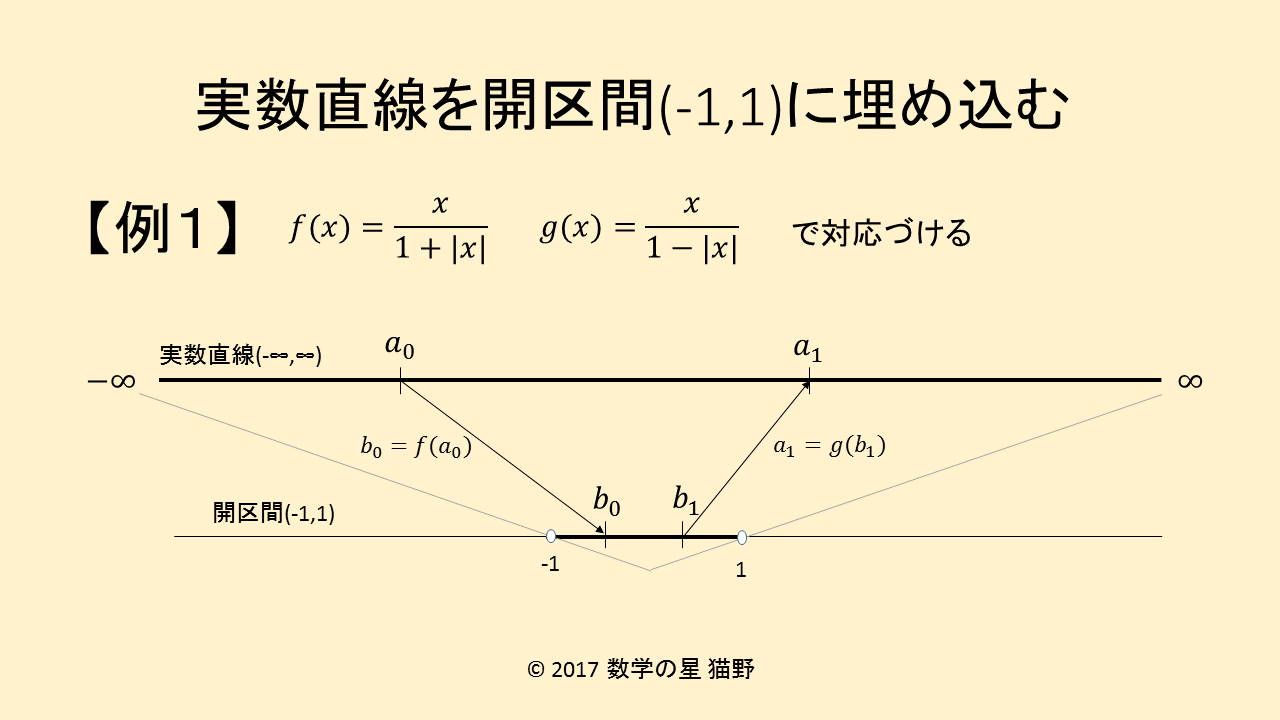
実数直線を二つの関数
\[f(x)=\frac{x}{1+|x|}\]
\[g(x)=\frac{x}{1-|x|}\]
によって、開区間(-1,1)と1対1に対応つけることができます。
数直線全体をぎゅ~っと縮めて開区間(-π/2,π/2)に対応させる
今度は角度を使って開区間(-π/2,π/2)に対応づけます。
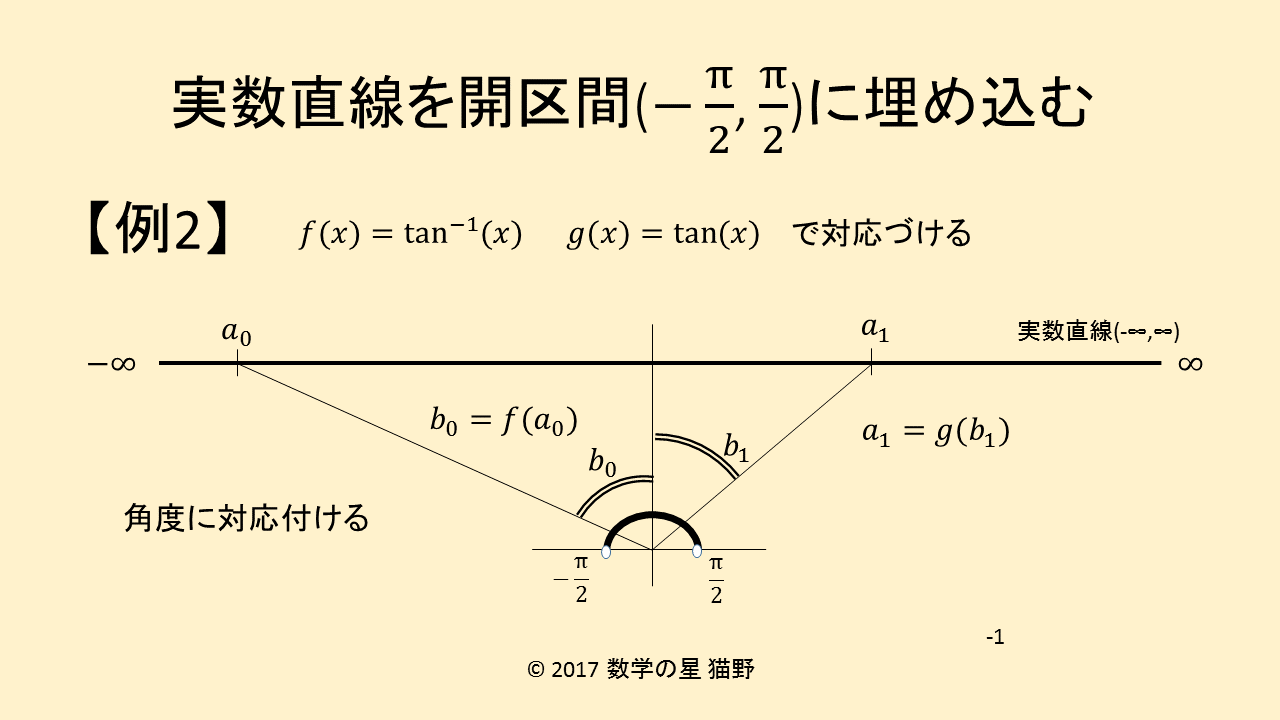
\[f(x)=\tan^{-1}(x)\]
\[g(x)=\tan(x)\]
によって、開区間(-π/2,π/2)と1対1に対応つけることができます。
比例定数π/2を使って縮小すれば、開区間(-1,1)にも対応づけることができます。
ラピディティ (Rapidity) を使った例
この他にも、物理学で使われているラピディティを使う方法があります。これは物理量ですから一層現実的です。
\[f(x)=\tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}\]
\[g(x)=\tanh^{-1}(x)\]
無限大(∞)は1に対応するのか
ここで、実数直線の端っこである、∞と-∞が開区間(-1,1)の端の1と-1に対応づけられそうです。
注意しておきたいのは、まだ上の関数f(x),g(x)では-1,1が定義域や値域に入っていません。拡張しようとしていますが。
なんとなく、1を正の無限大、-1を負の無限大として使えそうですね。
実数直線には、∞や-∞の点は含まれていませんが、開区間(-1,1)の端に対応する点として無理矢理実数直線の端に∞や-∞を拡張します。
この∞や-∞が実無限?
まあ、そうともいえますが、数として扱えるのでしょうか?
数の性質である、比較や演算がこの∞や-∞に対してどうなっているのか調べてみましょう。
[ad#foot]
参考
ちなみに、この実数直線を宇宙、開区間(-1,1)のことをこのサイトでは、「宇宙」「小宇宙」と呼んでいます。
また、ここででてくる「∞」のことを「(数の)ブラックホール」、「-∞」のことを「ホワイトホール」とも呼んでいます。
