[msg#wsiki]
\(n^{1/n}\)の極限を求める
問題
(1)\(\displaystyle 1+\frac{1 }{\sqrt{n}} \gt \sqrt[2n]{n}\)
n=1,2,3,…を証明せよ。
(2)\(\displaystyle \lim_{n \rightarrow \infty}{\sqrt[n]{n}}\)
をもとめよ。
解き方
(1)をつかって(2)を求めるように誘導されていますが、あるひらめきがないと手がつけられない問題となっています。
極限がわかっている数列で挟み込んで極限を求めるのですが、挟み撃ちする数列がそう簡単に思いつかないのです。
\((1+x)^n \gt nx\)
ここでは、
x>0、nが正の整数なら
\((1+x)^n \gt nx\)
を利用します。
この不等式は2項定理で証明できますが、
参考として「ベルヌーイ不等式」を利用して証明してみました。
\((1+x)^n \ge 1+nx \)
この「ベルヌーイ不等式」は数学的帰納法で証明できます。
略証
(1+x)(n+1)
=(1+x)n(1+x)
≧(1+nx)(1+x)
=1+nx+x+nx2
>1+(n+1)x
これを使えば、
\((1+x)^n \ge 1+nx \gt nx\)
指数の式を積の形に変形できるところがなんとも使える「ベルヌーイ不等式」です。
不等式\(n^{1/n}\ge 1\)
\(n^{1/n}\ge 1^{1/n}=1\)
という不等式も利用します。
略証
n≧1の両辺を1/n乗します。
解答
(1)の解答
(1)を証明します。
\(x=\frac{1}{\sqrt{n}}\)
と置くと、x>0ですから
\((1+x)^n>1+nx\)に代入すると、
\((1+\frac{1}{\sqrt{n}})^n\)
\(>n\frac{1}{\sqrt{n}}\)
\(=\sqrt{n}\)
n乗根をとると、
\(1+\frac{1}{\sqrt{n}}>=\sqrt[2n]{n}\)
証明終わり
(2)の解答
(2)を求める前に
(1)の不等式を2乗した不等式を得ます。
\((1+\frac{1}{\sqrt{n}})^2 \gt n^{1/n}\ge 1\)
両辺の極限をもとめると問題の数列は1に収束することがわかります。
答え 1に収束する。
他の数列の極限に関する問題:数列の極限の問題一覧
[ad#foot]
猫野の解析は

鉄則微分・積分
をテキストとして使っています。
鉄則ゼミ2の問題を解いています。



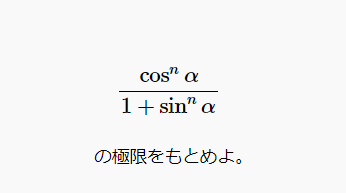
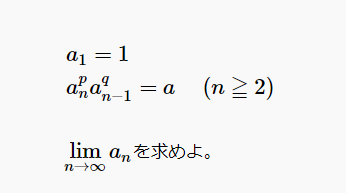
コメント