[msg#wsiki]
問題
\(\displaystyle a_1=2,\;a_{n+1}=\frac{1}{a_n}+\frac{a_n}{2}\; (n=1,2,\cdots)\)
のとき、数列\(\{a_n\}\)は極限\(\sqrt{2}\)をもつことを示せ。
解き方
極限がaであったとすると、
\(a=1/a+a/2\)となりますから
\(a^2=2\)
\(a=\pm \sqrt{2}\)
初期値からこの数列は極限\(\sqrt{2}\)であろうと推測できます。
そこで数列\(\{a_n-\sqrt{2}\}\)
が0に収束することを示す方法を考えます。
\(a_{n+1}-\sqrt{2}\)
\(=1/a_n+a_n/2 -\sqrt{2} \)
\(\displaystyle =\frac{2+a_n^2-2\sqrt{2}a_n}{2a_n} \)
\(\displaystyle =\frac{(a_n-\sqrt{2})^2 }{2a_n} \)
\(\displaystyle = \frac{a_n-\sqrt{2} }{2a_n} (a_n-\sqrt{2})\)
※うまく\(\displaystyle a_n-\sqrt{2}\)でくくれました。
\(\displaystyle = \frac{a_n-\sqrt{2} }{a_n} \frac{1}{2}(a_n-\sqrt{2})\)
\(a_n>\sqrt{2}\)
を示すと、
\(\displaystyle \le \frac{1}{2}(a_n-\sqrt{2})\)
となって等比数列の形になります。
解答
\(a_1>2\)
から\(a_n>0\)で
相加平均相乗平均の関係から
\(\displaystyle a_{n+1}=\frac{1}{a_n}+\frac{a_n}{2} \ge 2\sqrt{\frac{1}{a_n} \frac{a_n}{2}} = \sqrt{2} \)
であるので、
\(\displaystyle 0 \le \frac{a_n-\sqrt{2} }{a_n}<1\)
よって、
\(\displaystyle a_{n+1}-\sqrt{2}\le \frac{1}{2}(a_n-\sqrt{2})\)
より、
そこで数列\(\{a_n-\sqrt{2}\}\)
は公比(1/2)の等比数列であるから0に収束する。
よって、\(a_n\rightarrow 0\)
他の数列の極限に関する問題:数列の極限の問題一覧
[ad#foot]
猫野の解析は

鉄則微分・積分
をテキストとして使っています。
鉄則ゼミ6の問題を解いています。
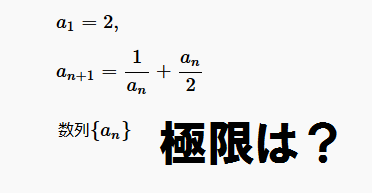


コメント