[msg#wsiki]
問題
行列
\(\displaystyle A = \left(
\begin{array}{cc}
a & b \\
1-a & 1-b
\end{array}
\right)
\)
のn個の積\(\displaystyle A^n\)は、
\(\displaystyle A^n=\left(
\begin{array}{cc}
a_n & b_n \\
1-a_n & 1-b_n
\end{array}
\right)
\)
の形になる。
ただし、\(b \ne 0、a-b \ne -1\)とする。
(1)
\(\displaystyle a_n, b_nをa,b,n\)で表わせ。
(2)
\(\displaystyle \lim_{n \rightarrow \infty} \frac{a_n}{b_n}\)
を求めよ。
(広島大)
解き方
本当にAnが問題文の形になるのか検証が必要なところですが、それが成立することを信じてAn+1とAnの関係を調べます。
An+1=AAnより
\(\displaystyle \left(
\begin{array}{cc}
a_{n+1} & b_{n+1} \\
1-a_{n+1} & 1-(b_{n+1})
\end{array}
\right)
\)
\(\displaystyle = \left(
\begin{array}{cc}
a & b \\
1-a & 1-b
\end{array}
\right) \left(
\begin{array}{cc}
a_n & b_n \\
1-a_n & 1-b_n
\end{array}
\right)
\)
\(\displaystyle =\left(
\begin{array}{cc}
aa_n+b-ba_n & ab_n+b-bb_n \\
1-(aa_n+b-ba_n) & 1-(ab_n+b-bb_n)
\end{array}
\right)
\)
成分を比較すると,
\(a_{n+1}=(a-b)a_n+b\)
\(b_{n+1}=(a-b)b_n+b\)
を得ます。
an,bnの漸化式が得られますから、この関係式(隣接2項間)からそれぞれの一般項を求めることができます。
a-b=1の時は、公差bの等差数列です。
\(a_n=a+(n-1)b\)
\(b_n=b+(n-1)b\)
a-b≠1のときは、
\(\displaystyle \alpha = \frac{b}{1-a+b} \)とおくと、
\(\displaystyle a_{n+1}-\alpha=(a-b)(a_n-\alpha)\)
となって等比数列になりますから、
\(a_n-\alpha=(a-\alpha)(a-b)^{n-1}\)
同様にして、
\(b_n-\alpha=(b-\alpha)(a-b)^{n-1}\)
を得ます。
解答
(1)の解答例
An+1=AAnより成分を比較すると、
\(a_{n+1}=(a-b)a_n+b\)
\(b_{n+1}=(a-b)b_n+b\)
となる。
a-b=1の時は、公差bの等差数列で、
\(a_n=a+(n-1)b=1+nb\)
\(b_n=b+(n-1)b=nb\)
a-b≠1のときは、
\(\displaystyle \alpha = \frac{b}{1-a+b} \)とおくと、
\(\{a_n-\alpha\},\{b_n-\alpha\}\)は等比数列で、
\(a_n-\alpha=(a-\alpha)(a-b)^{n-1}\)
\(b_n-\alpha=(b-\alpha)(a-b)^{n-1}\)
となり、これを整理すると、
\(\displaystyle a_n= \frac{(1-a)(a-b)^n+b}{1-a+b}\)
\(\displaystyle b_n=\frac{-b(a-b)^n+b}{1-a+b}\)
となる。
(2)の解答例
<場合1>a-b=1のとき、
\(\displaystyle \frac{a_n}{b_n}\)
\(\displaystyle =\frac{1+nb}{nb}\)
\(\displaystyle =\frac{1/n+b}{b}\)
より、
\(\displaystyle \lim_{n \rightarrow \infty} \frac{a_n}{b_n}=1\)
<場合2>a-b≠1のとき、
\(\displaystyle \frac{a_n}{b_n}\)
\(\displaystyle =\frac{(1-a)(a-b)^n+b}{-b(a-b)^n+b}\)
となる。
<場合3>|a-b|<1のとき、
\(\displaystyle \lim_{n \rightarrow \infty} \frac{a_n}{b_n}=\frac{b}{b}=1\)
<場合3>|a-b|>1のとき、
\(\displaystyle \lim_{n \rightarrow \infty} \frac{a_n}{b_n}\)
\(\displaystyle =\frac{(1-a)+b/(a-b)^n}{-b+b/(a-b)^n}\)
\(\displaystyle =\frac{1-a}{-b}\)
\(\displaystyle =\frac{a-1}{b}\)
以上をまとめて、
答え
-1<a-b≦1のとき、1
|a-b|>1のとき、\(\displaystyle \frac{a-1}{b}\)
コメント
この問題は行列で与えられていますが、漸化式をつくるときに行列の計算をしたものの、行列の性質は使わずに解けました。
他の数列の極限に関する問題:数列の極限の問題一覧
[ad#foot]
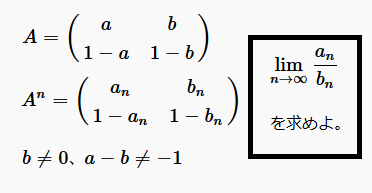



コメント