\( \log\)の記号がついている場合には、暗に真数条件が指定されています。
真数条件とは
\( \log_a x\)と書かれていると、暗に\(x \gt 0\)が仮定されているということです。
\( \log_a x\)の\(x\)の部分が真数と呼ばれているので、この条件のことを真数条件といいます。
よくあるのは、例えば
\( \log_a (x^2-1)\)といった式が合った場合、
\(x^2-1>0\)が暗に仮定されているということになります。
この場合言い換えると、\(x<-1\) または \(1<x\)を暗に仮定して考える必要があります。
なぜなら、例えば真数条件を満たさないx=0では\(\log\)の意味(定義)がないからです。
例1
\( \log_a (x^2-1)\)
と
\( \log_a (x-1)+\log_a(x+1)\)
両者は似たように思えますが、定義されているxの範囲は違います。
\( \log_a (x^2-1)\)は、
\( \log_a (x-1)+\log_a(x+1)\)
を変形した式に見えますが真数条件が違っているからです。
\( \log_a (x^2-1)\)と書かれている場合の真数条件は、
\(x<-1\) または \(1<x\)です。
\( \log_a (x-1)+\log_a(x+1)\)の場合の真数条件は、
\(x-1>0\)かつ\(x+1>0\)です。
したがって、\( \log_a (x-1)+\log_a(x+1)\)と書かれている場合は、
\(x>1\)を真数条件として考える必要があります。
logの式変形する時は、真数条件を考えて行う必要があります。
例2
\(\displaystyle \log_a \left(\frac{x+1}{x-1}\right)\)
と
\( \log_a (x+1)-\log_a(x-1)\)
の場合も同様に\(x\)の範囲は、違った条件が仮定されます。
\(\displaystyle \log_a (\displaystyle \frac{x+1}{x-1})\)
の真数条件は、
\(x\ne1\)で\(\frac{x+1}{x-1}>0\)が真数条件です。
これは、わかりやすく変形すると、
\(x<-1\)または\(x>1\)が真数条件です。
一方、
\( \log_a (x+1)-\log_a(x-1)\)の場合は、
\(x+1>0\) かつ \(x-1>0\)、
すなわち\(x>1\)が真数条件になります。
意外と真数を注意深く検証しなければ落とし穴に陥ってしまう可能性があります。
底の条件
\( \log\)には、真数条件だけでなく底の条件というのもあります。
通常は底は固定して考えることが多いのであまり注目されないのですが、底が変数(定数でない)場合には注意が必要です。
\( \log_a x\)の底の条件は、
\(a>0,a\ne 1\)
になります。
\(a>0,a\ne 1\)の場合には、\(\log_a x\)がうまく定義できないからこのような条件がつきます。
[ad#foot]
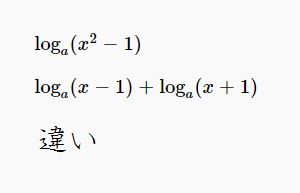



コメント
最後のとこ
案外→意外 では?
それ以外は見やすかった
訪問ありがとうございます。
「案外」にそれほど深い意味はないので、「意外」に直しました。
これからも精進いたします。
問題を回答するときに、進数条件という言葉が必要だとききましたが、進数関係という言葉でもいいのでしょうか?
質問ありがとうございます。
「[進]数条件」と書かれていますが「[真]数条件」の書き間違え(変換ミス)でしょうか?
私は、これまで進数関係という用語(言葉)は聞いたことないです。
(ちなみに「進数条件」という用語も聞いたことはないです。少なくとも対数関数では。)
ですので、こういった問題では、進数関係という言葉は使わないほうがよいと思います。
意味が通じないと思いますから。
真数条件とは、「対数関数logが意味を持つための条件」という意味ですから、
やはり条件という言葉がしっくりきます。
進数関係といわれると、例えば、10進数と2進数の関係のことかな?
といった意味で考えてしまいます。
ですので、私の結論は、
進数関係という言葉はダメ、真数条件という言葉が必要となります。
例2の真数条件に関してですが、
真数条件一つしかありませんが、2つあると思います。