関数\(\sqrt{\tan(x)}\)の微分です。
関数\(\sqrt{\tan(x)}\)の微分(導関数)
\(\sqrt{\tan(x)}\)の微分は、
\(\sqrt{f(x)}\)の微分公式を使って計算します。
\(\sqrt{f(x)}\)の微分公式
\(\displaystyle \sqrt{x}=x^{1/2}\)の微分は、
\(\displaystyle (x^{\frac{1}{2}})’\)
\(\displaystyle =\frac{1}{2}x^{ -\frac{1}{2} }\)
\(\displaystyle =\frac{1}{2\sqrt{x}}\)ですから、
\(\sqrt{f(x)}=f(x)^{ \frac{1}{2} }\)の微分は合成関数の微分公式より、
\( ( f(x)^{ \frac{1}{2} } )’ \)
\(\displaystyle =\frac{1}{2\sqrt{f(x)}}(f(x))’\)です。
これで準備ができました。
\(\sqrt{\tan(x)}\)の微分
\(\sqrt{\tan(x)}\)の微分は、
\(f(x)=\tan(x)\)として、上記の公式を使います。
\(\tan(x)\)の微分は、\(\sin(x)\)、\(\cos(x)\)の微分公式と商の微分公式から計算できます。
\((\tan(x))’\)
\(\displaystyle =\left(\frac{\sin(x)}{\cos(x)}\right)’\)
\(\displaystyle =\frac{(\sin(x))’\cos(x)-\sin(x)(\cos(x))’}{\cos(x)^2}\)
\(\displaystyle =\frac{\cos(x)\cos(x)+\sin(x)\sin(x)}{\cos(x)^2}\)
\(\displaystyle =\frac{1}{\cos(x)^2}\)
です。
\((\sqrt{\tan(x)})’\)
\(\displaystyle =\frac{1}{2 \sqrt{\tan(x)}} (\tan(x))’\)
\(\displaystyle =\frac{1}{2 \sqrt{\tan(x)}} \frac{1}{\cos(x)^2}\)
\(\displaystyle =\frac{1}{2 \cos(x)^2 \sqrt{\tan(x)}}\)
が答えです。
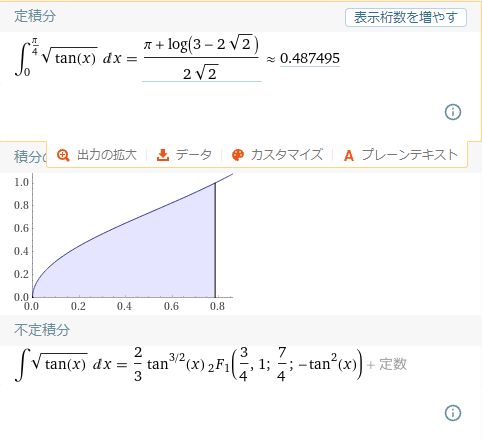
微分はわりと公式で簡単に解けますが、積分はやり方を知らないとお手上げです。