超越数とは、代数的でない複素数の事です。
名前が超実数と似ていますが、超実数とは全然違う概念の数です。また、無理数ともちょっと違います。
超越数の定義
超越数とは代数的数でない数の事ですから、
超越数の定義を知るために代数的数の定義を知る必要があります。
代数的数とは、整数係数の方程式の解になりえる複素数の事です。
例えば、代表的な代数的数の例を挙げると、\(\sqrt{2}\)があります。
簡単な例として、ルートが付いている数は、代数的数になります。したがって、ルートが付いている数は超越数ではありません。
代数的数の定義
\(a_0,a_1,\cdots,a_n\)を整数としたとき、
\(a_0 +a_1 x+\cdots+a_nx^{n}=0\)の解を代数的数という。
係数が整数になっているところは重要です。
\(\sqrt{2}\)は、\(x^2-2=0\)の解になりますから、代数的数と言うわけです。
整数係数の2次方程式、3次方程式の解はもちろん、4次、5次の方程式の解もすべて代数的数です。
有理数(分数)も、(整数係数の)1次方程式の解になりえますから、代数的数です。
したがって、代数的数は有理数をすべて含みます。
また、虚数単位\(i\)も、\(x^2+1=0\)の解の一つですから、代数的数です。
代数的数は実数とは限りません。実数でない代数的数もあります。
代数的数の中で実数のものを、実代数的数という事もあります。
代数的数がわかれば、それ以外の複素数が超越数ですから、超越数の事もわかったことになります。
実数の中で有理数でない数を無理数と呼びますが、有理数は代数的数、すなわち超越数ではありませんから、実数である超越数は無理数であることになります。
超越数の代表例
超越数の代表的な数は、円周率\(π\)です。
これが一番有名な超越数です。
2番目に有名な超越数は、自然対数の底として使われるネイピアの数\(e\)です。
超越数は、山ほどあるのですが、与えられた数が超越数かどうか判定することが極めて難しいため、例も挙げるのも簡単にはいきません。
実際によく知られている超越数は、\(e\)や\(π\)に関係するものが多いですが、これ以外に有名なのはリウヴィル数です。
超越数について研究する第一歩は、リウヴィル数です。
円周率やネイピア数が超越数であることは有名ですが、その証明は簡単でありません。
それに比べて、リウヴィル数が超越数であることは、わりと簡単に示せます。
また、このリウヴィル数から超越数の研究が始まったとも言えます。
リウヴィル数は、超越数であること以外には、数学の中でもほとんど出現することがない数ですが、この数によって超越数の性質が少しあらわになりました。
代数的数でない事を示す事がはなはだ困難である数のなかから、超越数を選ぶ簡単な方法がリウヴィル数を使う事です。
特に、
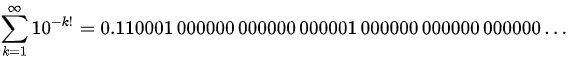
は最も有名なリウヴィル数です。
これは、小数点以下がほとんど0なのですが、1桁目、2桁目、6桁目、24桁目、n!桁目の部分だけ1になっている無限小数で表される実数です。
超越数の濃度
超越数がどれくらい多く存在しているかどうかは、濃度の議論で簡単にわかります。
すなわち、代数的数の濃度が加算であることがわかるので、これから超越数は実数の濃度で存在することになります。
すなわち、ほとんどすべての複素数は超越数であるわけです。
\(π+e\)が超越数かどうかは未解決問題の一つとなっていますが、確率的には超越数である可能性がすこぶる高いといえます。
