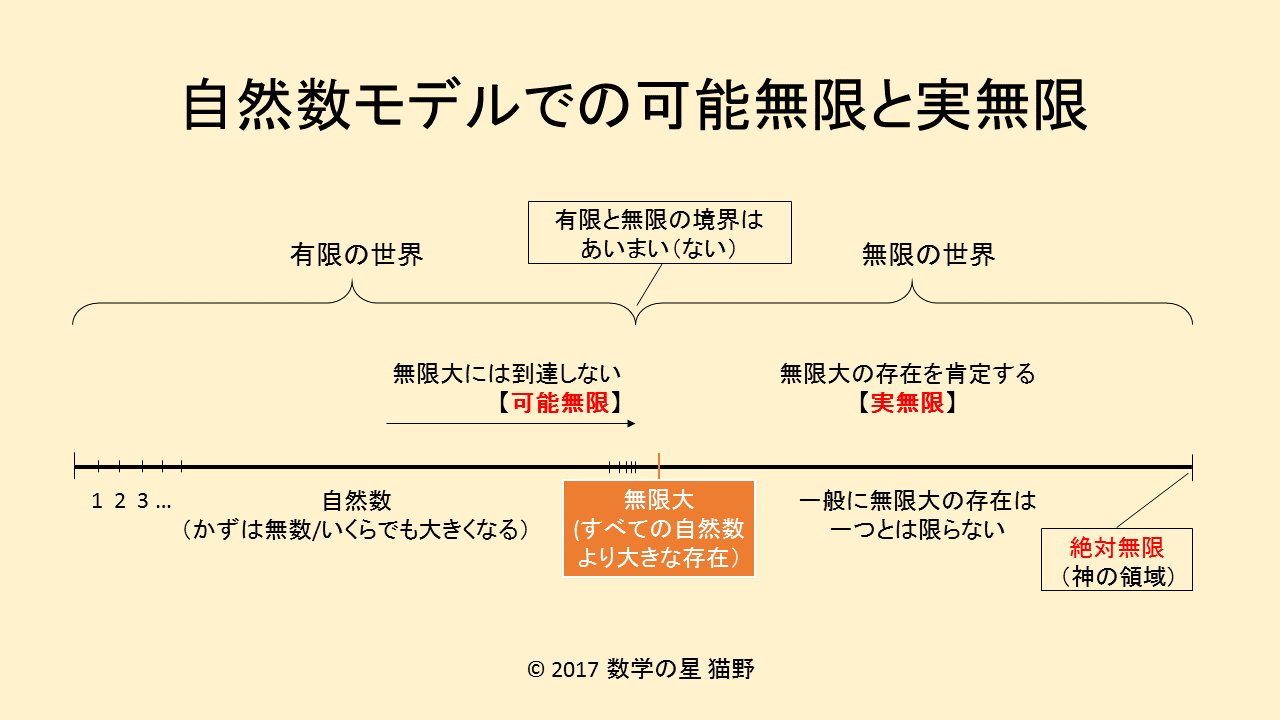
可能無限と実無限を表した図
このサイト管理者が考えている可能無限(仮無限、潜在的無限)と実無限の意味を図で説明することにしました。自然数を例にして、可能無限と実無限を図(下の方に掲載)を使って解説します。
可能無限と実無限の図を使った説明
1.まず、数の世界を、その存在の有無は別にして「有限の世界」「無限の世界」とに分けます。
2.有限の世界は、認知できる数の事で、自然数がそれに該当します(ここでは負の数は考えていません)。図では、自然数が順序よく並べられていて、右にいくほど大きな自然数を表しています。
3.自然数の先(果て)があるかどうかは、つまり、無限の世界があるかどうかは、考え方の違いになります。
3.無限の世界にあるものを無限大(具体的概念に置き換える場合は極限順序数と言い換える)と呼んでいます。無限大の世界があるということは、すくなくとも一つの無限大が存在することを肯定するということです。
4.可能無限の考え方では、無限大の世界があるのかどうかは問いませんが、自然数はいくらでも大きくなるので、無限大が存在する可能性は肯定します。
5.無限の世界があると考えるのが「実無限」での考え方です。実無限の考え方もバリエーションがいろいろあります。
6.無限大の中でも、最大の無限大という存在を考える人もいます。そのような無限大は絶対無限と呼ばれています。この無限大は特殊で、これ以上増えません。固定です。足しても掛けてもこれ以上大きくならない無限大が絶対無限です。神学的立場で考える数としてこのような絶対無限の存在が肯定されることがあります。
6.無限大は1つしかないと考える考え方です。つまり、無限の世界で存在する無限大は一つです。これは、絶対無限だけの存在を肯定している考え方と同じといえます。
7.大多数の実無限支持者は、無限の世界に無限大が幾種もあると考えています。
8.無限大の可能性すら否定する考え方も有りえます。この考え方も実無限に対抗する考え方になりますので可能無限に含まれることになりますが、私は、そのような極端な考え方は排除したいので、無限大の可能性すら否定する考え方を不可能無限と呼んでいます。この考え方の支持者は、物理特性によって無限を否定しているようです。物性として無限の存在を否定し、人間の思考も(脳が物質からできているので)、その物性の束縛から開放されるはずがなく、現実として無限について考えることすらできないと考えます。なんでもかんでも有限であるという考え方です。自然数も無限に数えることができません。この考え方で数を考えるのは、きわめて乏しい数の体系しか生み出せないはずです。
9.実無限の支持者でもよく混乱があります。簡単に避けられる混乱もあれば、悩ましい混乱もあります。これが無限のつかみどころのない不思議な性質で、無限の存在を揺るがす場合もあります。
10.この例のように、自然数の大きさだけに限定して考えてるうちは、シンプルに無限のことを考えることができますが、無限と無限が組み合わさったり、実数のように大きい方だけでなく細かい方の世界も含めて考えると、さらにバリエーションが膨れてきます。つまり、εーN(イプシロン-エヌ)よりεーδ(イプシロンーデルタ)のほうが複雑なように、無限を組み合わせることで複雑さが倍増するのです。
11.有限と無限の境界が曖昧というのを最後に説明します。無限の最大値については絶対無限という考え方があることを示しましたが、逆に無限の最小値についてはどうかという問題(命題)が生じます。絶対無限を絶対最大無限といいかえるのであれば、絶対最小無限という考え方もできますが、これについて調べてみたところ、あまり重要視されていないようです。個人的には無限大に関しても数として扱う限り、比較や四則演算を導入するので、境界はないと考えてます。
12.本来の実無限の考え方は、有限を超越する一つの存在としての無限だったように思います。アキレスが亀に追いつくように、ある行為を無限回を繰り返すことで到達し得ないある地点に到達することができる、その無限回に相当する数が実無限の発想の始まりといえます。これは素朴な発想であり、極めて自然な考え方といえます。しかし、実際そのような無限回を表すような数を考えることで数の体系がボロボロになってしまうのです。無限回は神の領域として触れないでおこう、これも一つの考え方ですが、そうあっさりとは割り切れないのです。
無限の話は哲学者に任せるべきか
哲学者のほうが、もっと詳しく、深く無限について考察されています。それも、相当な歴史があります。可能無限と実無限について、その違いや混同について、そう簡単に説明できるものではない事をくどくど書いている理由はなにか。
それは、数の体系を見直すためです。哲学者も数について考えています。その歴史が今の数学で使われていますが、完成しているとは言い難い面もあります。そのなかでも、無限についての取扱は数の世界でも確立半ばといえます。
発端は微分積分にあります。無限大、無限小のからくりをもっと解明するために、無限の知識を整理する必要があるのです。哲学者はそこまで考えてくれませんでした。考えたのかもしれませんが、いまだ完成とはいえません。せめて数の世界だけでも無限の扱いを整備したいのです。
[ad#foot]
