数学者ゲルシュゴリンはあまり知られていませんが、その名を冠したゲルシュゴリンの円盤定理は、行列解析において非常に強力な手段となります。本記事では、この定理をご紹介します。
ゲルシュゴリン円盤定理
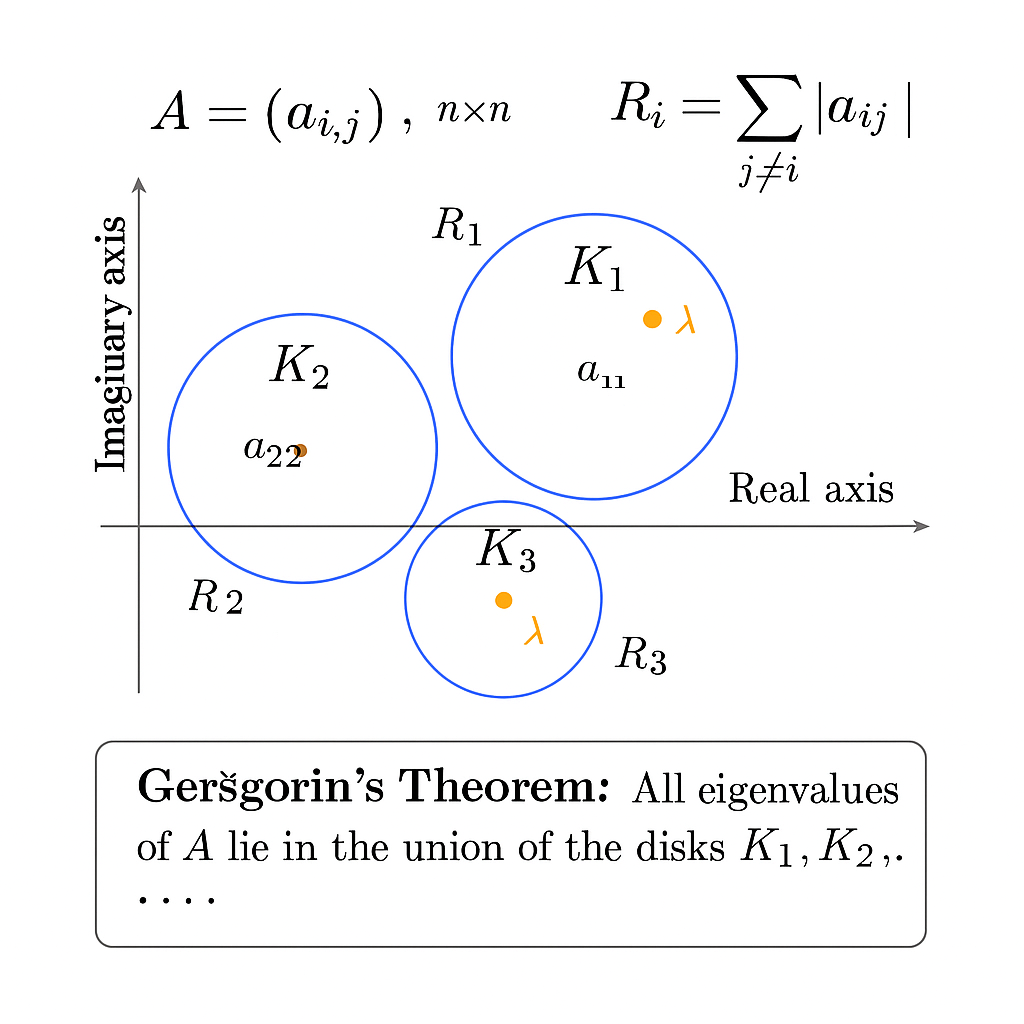
行列の固有値が複素平面上のどこに存在するかを制限する基本定理として、ゲルシュゴリン円盤定理があります。
正方行列 \( A = (a_{ij})_{n \times n} \) を考えるとき、各行に対して次の円盤を定義します。
中心: \( a_{ii} \)
半径: \( R_i = \sum_{j \neq i} |a_{ij}| \)
このとき、円盤 \( K_i = \{ z \in \mathbb{C} : |z – a_{ii}| \leq R_i \} \) を ゲルシュゴリン円盤 と呼びます。
定理(ゲルシュゴリン, 1931):
行列 \( A \) のすべての固有値は、円盤 \( K_1, K_2, \dots, K_n \) の和集合に含まれる。
解説
この定理の直感的な意味は「行列の固有値は、対角成分の近くに現れるが、そのずれは非対角成分の大きさに制限される」ということです。
もし円盤が互いに重なり合えば、その領域には複数の固有値が存在する可能性があります。逆に、孤立した円盤には必ず対応する固有値が1つだけ存在します。
この幾何学的な視点は、数値解析や安定性解析において非常に有用であり、行列の性質を直感的に理解する助けとなります。
各定理の証明の骨子
ここでは、ゲルシュゴリン論文に現れる主要定理の「証明の骨子(キーアイデアと要点)」を簡潔に展開します。厳密証明の全細部ではなく、読者が論理の流れを把握しやすいように、核心となる不等式・構成・連続性の議論を中心に整理しています。
補題(対角優位による非特異性)
主張: 各行で \( |a_{ii}| \ge \sum_{j\ne i} |a_{ij}| \) が成り立ち、少なくとも一行で不等号が厳密(>)なら、行列 \( A \) は可逆(\( \det A \ne 0 \))。
- 最大成分の選択: \( Ax=0 \) に非零解があると仮定し、\( |x_k| \) が最大となる添字 \( k \) を選ぶ。
- 第\( k \)行の式: \( a_{kk}x_k + \sum_{j\ne k} a_{kj} x_j = 0 \) より、\( |a_{kk}|\,|x_k| \le \sum_{j\ne k} |a_{kj}|\,|x_j| \le \big(\sum_{j\ne k} |a_{kj}|\big)|x_k| \)。
- 矛盾の導出: もし \( |a_{kk}| > \sum_{j\ne k} |a_{kj}| \) なら上の不等式と矛盾。すべての行で等号のみなら、別行の厳密不等号が必要という仮定に反する。
- 結論: 仮定は誤り。したがって \( \det A \ne 0 \)。
定理 I(ゲルシュゴリン円盤定理)
主張: 固有値 \( \lambda \) は、各行の円盤 \( K_i = \{ z\in\mathbb{C}:\ |z-a_{ii}|\le R_i\}\)(\( R_i=\sum_{j\ne i}|a_{ij}|\))の和集合に含まれる。
- 固有ベクトルの最大成分: \( Ax=\lambda x \) の非零解 \( x \) に対して、\( |x_k| \) 最大の添字 \( k \) を取る。
- 第\( k \)行の式: \( (a_{kk}-\lambda)x_k = -\sum_{j\ne k} a_{kj}x_j \) から、\( |a_{kk}-\lambda|\,|x_k| \le \sum_{j\ne k}|a_{kj}|\,|x_j| \le R_k |x_k| \)。
- 半径境界: \( |a_{kk}-\lambda| \le R_k \)、すなわち \( \lambda \in K_k \)。
- 結論: 固有値は少なくとも一つの円盤に属する。
定理 II(連結成分ごとの個数)
主張: 円盤の連結成分 \( H(m) \)(\( m \)個の円盤が重なって形成)には、正確に \( m \) 個の固有値が含まれる。
- 連続変形の設定: 非対角成分を 0 から元の値まで、各行ごとに単調に増やす連続パラメータ \( t\in[0,1] \) をとる。
- 開始点のスペクトル: \( t=0 \) の対角行列では固有値は各中心 \( a_{ii} \) にあり、\( H(m) \) に属するものはちょうど \( m \) 個。
- 円盤の分離維持: 連続変形中、\( H(m) \) を構成する円盤群は他の円盤群と交差しないように半径を単調増加させても境界の分離を保つ。
- 固有値の連続性: 固有値は行列成分の連続関数として分枝しつつも全体個数は不変。\( H(m) \) から外へ連続的に飛び出すには外部円盤群との境界交差が必要だが、それは起きない設定。
- 結論: 変形全期間にわたり \( H(m) \) 内の固有値の個数は \( m \) に保たれる。
定理 III(円盤が互いに素で実行列なら固有値は実)
主張: \( A \) が実行列で、各ゲルシュゴリン円盤が互いに交わらず分離しているとき、固有値はすべて実数。
- 共役対の性質: 実係数行列の固有値が複素なら、必ず共役対 \( \lambda, \overline{\lambda} \) で出現。
- 円盤配置の制約: 非交差のため、各連結成分が単一円盤に一致し、定理 II により各円盤内の固有値個数は 1。
- 矛盾の導出: 1 個しか入れない円盤に共役2個は同時に入れられない。したがって各円盤の固有値は実数である必要がある。
- 結論: 全固有値は実。
拡張(列版ゲルシュゴリン円盤と相似変換による改良)
主張: 行版に加え、列に基づく円盤(中心 \( a_{ii} \)、半径 \( C_i=\sum_{j\ne i}|a_{ji}| \))も固有値を包含する。さらに、適切な相似変換により円盤の形状(半径配分)を改善でき、包含領域を狭められる。
- 列版の導出: 固有方程式 \( A^T y = \lambda y \) に対して行版の議論を適用すると列半径版が得られる。
- 相似変換: 対角行列 \( S=\mathrm{diag}(s_1,\dots,s_n) \) で \( B=SAS^{-1} \) を構成。\( b_{ij}= (s_i/s_j)a_{ij} \) により、行半径 \( R_i(B)=\sum_{j\ne i}|b_{ij}| \) を制御。
- 重み付けの意図: 特定の行群の半径を縮め、他行群の半径を許容的に増やすことで、関心領域の円盤を他と分離しつつ狭める(スペクトルは相似で不変)。
- 結論: 行版・列版・重み付き相似版の交わりをとれば、包含領域がより鋭くなる。
孤立円盤の精密化(半径の更なる縮小)
主張: ある円盤 \( K_i \) が孤立しているとき、適切な対角相似変換により同心のより小さい円盤に固有値の位置を絞り込める。
- 設定: 孤立円盤 \( K_i \) を含む行群に対し、\( S=\mathrm{diag}(s_1,\dots,s_n) \) を用いて \( s_i \) を他より小さく(もしくは大きく)選び、\( b_{ij}=(s_i/s_j)a_{ij} \) によって半径を縮小。
- 非交差維持条件: 半径の調整は、他の円盤と交差しない範囲で行う(外接までは許容)。孤立性が保たれるため、定理 II の「個数 1」が維持される。
- 新半径の評価: 調整後の行半径 \( R_i’=\sum_{j\ne i} |(s_i/s_j)a_{ij}| \) を最小化するよう \( s_j \) を選ぶことで、包含円盤を厳密に縮める。
- 結論: 固有値は元の中心 \( a_{ii} \) を中心とするより小さい円盤に入る。
補足(証明技法のキーポイント)
- 最大成分法: 固有ベクトルの最大成分に注目することで、行ごとの不等式から円盤包含を導く。
- 連続性の利用: 固有値の連続依存性と円盤の分離維持を組み合わせ、連結成分内の個数不変を示す。
- 相似不変性: 相似変換でスペクトルは不変だが、半径は変わる。目的に合わせて重み付けし、境界を鋭化する。
- 共役対の排除: 実行列+円盤非交差の仮定下では、共役2個を収容できないため、実固有値のみが残る。
ゲルシュゴリンによる固有値の位置の境界(1931)
著者: S. ゲルシュゴリン
出典: Bulletin de l’Académie des Sciences de l’URSS, 1931, Issue 6, pp. 749–754
この論文では、行列の固有値が複素平面上のどの領域に存在し得るかを示す方法が提示される。これは後に「ゲルシュゴリンの円盤定理」と呼ばれ、線形代数学や数値解析における基本的な道具となった。
§1 基本的な考え方
複素数を成分とする正方行列 \( A = (a_{ij}) \) を考える。固有値は特性方程式 \( \det(A – \lambda I) = 0 \) の解として定義される。
従来の研究では固有値の大きさに関する粗い上界しか得られていなかったが、ゲルシュゴリンはより精密に「固有値が存在する領域」を幾何学的に示した。
§2 ゲルシュゴリン円盤定理
各行について、対角成分 \( a_{ii} \) を中心とし、半径 \( R_i = \sum_{j \neq i} |a_{ij}| \) の円盤 \( K_i \) を複素平面上に定義する。
定理 I: 行列 \( A \) のすべての固有値は、円盤 \( K_1, K_2, \dots, K_n \) の和集合に含まれる。
§3 円盤の重なりと固有値の分布
もし複数の円盤が重なり合い、連結な領域 \( H(m) \) を形成するならば、その領域にはちょうど \( m \) 個の固有値が含まれる。
したがって、円盤の配置を調べることで、固有値の数や分布を推定できる。
§4 実行列の場合
行列の成分がすべて実数であり、円盤が互いに交わらない場合、固有値はすべて実数である。
§5 改良と拡張
行に基づく円盤だけでなく、列に基づく円盤を用いることもできる。また、行列に適切な相似変換を施すことで、より鋭い境界を得ることが可能である。
§6 孤立した円盤の場合
もしある円盤 \( K_i \) が他と交わらず孤立しているならば、その円盤内には必ず対応する固有値が一つだけ存在する。さらに、より小さな同心円盤に固有値が含まれることも示される。
結論
ゲルシュゴリンは、行列の固有値の位置を幾何学的に直感的かつ厳密に制限する方法を提示した。この結果は、数値解析や安定性解析において現在も広く利用されている。
