 数学問題
数学問題 微分の定義に従って解く問題
微分の定義がよくわかっていないと解けない(解けたと言えない)問題です。
 数学問題
数学問題  猫野の微分積分
猫野の微分積分 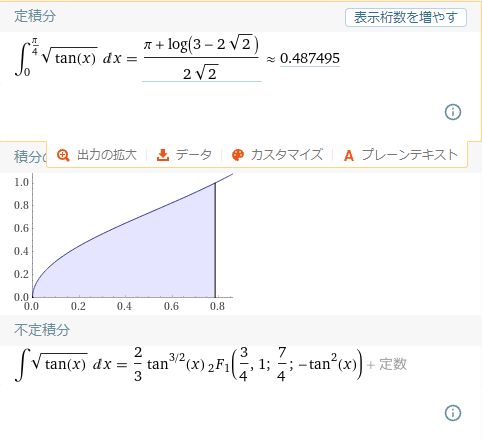 猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分