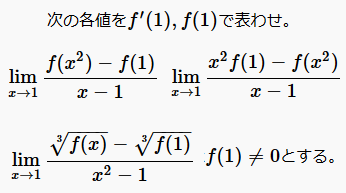 猫野の微分積分
猫野の微分積分 合成関数の微分公式を使って解く極限の問題
問題次の各値を\(f^{\prime}(1),f(1)\)で表わせ。ただし、(3)では\(f(1)\ne 0\)とする。(1)\(\displaystyle \lim_{x \rightarrow 1}\frac{f(x^2)-f(1)}{...
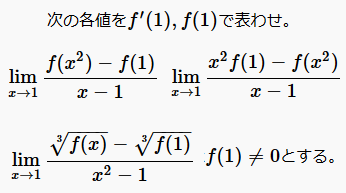 猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分  数論
数論  猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分  代数
代数  代数
代数  猫野の微分積分
猫野の微分積分