パソコンのお絵かきソフトで線を引きながら考えました。適当に線を引いていると、交わってしまのですが、できるだけ長く引くように頑張ります。交わらないように線を引いていても、この線には太さがあるのでいつかは限界がきて線と線が触れてしまいます。

真面目な数学の問題です。
一辺が1の正方形があるとします。
この正方形の中に(連続している)線を引きます。ただし、線は交わってはいきません。
どれだけ長く線を引けるか。
線の太さは考えませんが、線と線が接したり、交差したりすることは許されません。
(私の考えた答えのようなもの)
線には幅がないので、無限の長さの線が引ける。
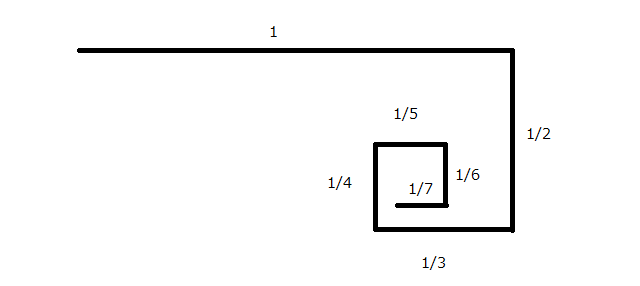
まず、左上頂点から右に向かって長さ1の線を引きます。
右上から下に向かって長さ1/2の線を引きます。
右下から左に向かって長さ1/3の線を引きます。
左下から上に向かって長さ1/4の線を引きます。
左上から右に向かって長さ1/8の線を引きます。
・・・
こうやって引いた線の長さは、
\[ 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\cdots \]
この級数は発散するので、無限に長い線が引けることがわかります。
答え
有限の領域に無限に長い線を引くことができる。

コメント