任意の複素数zは、長さrと偏角tで下記のように表すことができます。
\(\displaystyle z=r(\cos t +i \sin t)\)
二つの複素数を掛け算すると、長さは長さ通しの積、偏角は和で表される複素数になります。
特に長さ1の複素数を複素数に掛け算するということは、その複素数を偏角の分回転することになります。
単に虚数単位iを追加しただけの複素数ですが、このような性質があるのです。
不思議ですね。
これは、複素平面ならではの最大の特徴とも言えます。
単なる平面も複素平面として捉えると、掛け算が回転に対応する素晴らしい性質がゲットできるのです。
回転行列
平面座標で、回転する一次変換、つまり回転行列というのがあります。
回転角をθとすると、回転行列は、
\(\displaystyle \begin{pmatrix} \cos t & -\sin t \\ \sin t & \cos t \end{pmatrix} \)
で表せれます。
この行列で、座標(a,b)で表される平面座標の点を角度t(ラジアン)回転した座標を次の行列計算で求めることができます。
\(\displaystyle \begin{pmatrix} \cos t & -\sin t \\ \sin t & \cos t \end{pmatrix} \begin{pmatrix} a \\ b \end{pmatrix} \)
これを計算すると、
\(\displaystyle \begin{pmatrix} a \cos t – b\sin t \\ a \sin t +b \cos t \end{pmatrix} \)
となりますから、回転した座標は、
\(\displaystyle (a \cos t – b\sin t, a \sin t +b \cos t )\)
となります。
複素数の掛け算で回転
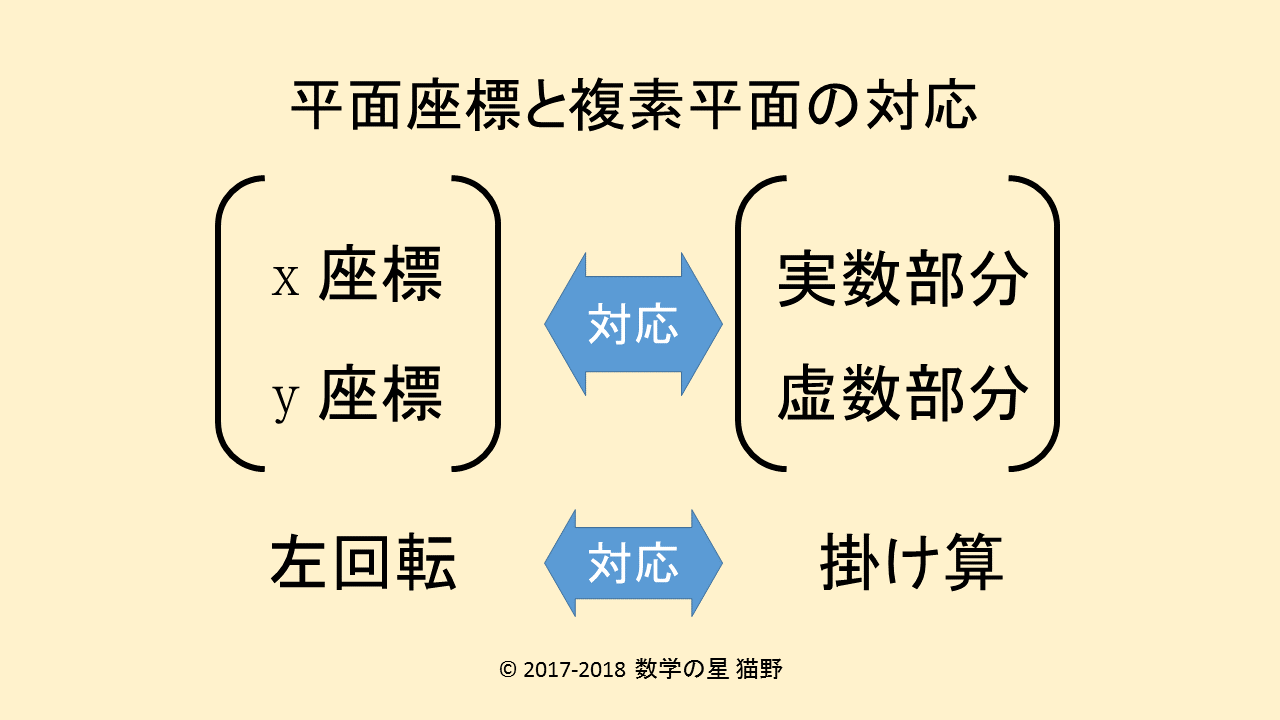
平面座標と、複素平面の対応は、次のようになります。
平面座標のx座標は、複素平面の実数部分
平面座標のy座標は、複素平面の虚数部分
したがって、式でかくと、
座標(a,b)は、\(a+bi\)
に対応するわけです。
複素数a+biを回転角tだけ反時計回りに回転させた複素数は、
長さ1で偏角tの複素数をかければよいです。
つまり、\(a+b i\)に\(\displaystyle \cos t + i \sin t\)
をかければよいのです。
複素数の掛け算をしてみますと、
\(\displaystyle (a+bi)( \cos t + i \sin t)\)
\(\displaystyle =(a \cos t -b \sin t ) +(a \sin t + b \cos t)i\)
となって、実数部分をx座標、虚数部分をy座標に対応させると、
みごとに、先ほど回転行列をつかって求めた
\(\displaystyle (a \cos t – b\sin t, a \sin t +b \cos t )\)
の座標と一致していることが確認できます。
複素平面を使えば、回転行列を使わなくても、回転座標を素早く求めることができるのです。
なんて複素平面は便利なのでしょう。
[ad#foot]


コメント