 代数
代数 複素数を使った多項式の因数分解
因数分解の公式はよく教科書にわかりやすく載っていますが、複素数をつかった因数分解の公式はあまり載っていません。最も簡単な例は、\(\displaystyle a^2+b^2\)の因数分解です。3乗多項式の展開と因数分解公式複素数の因数分解を...
 代数
代数  代数
代数  代数
代数  代数
代数  代数
代数  無限
無限  無限
無限  実数の作り方
実数の作り方  無限
無限 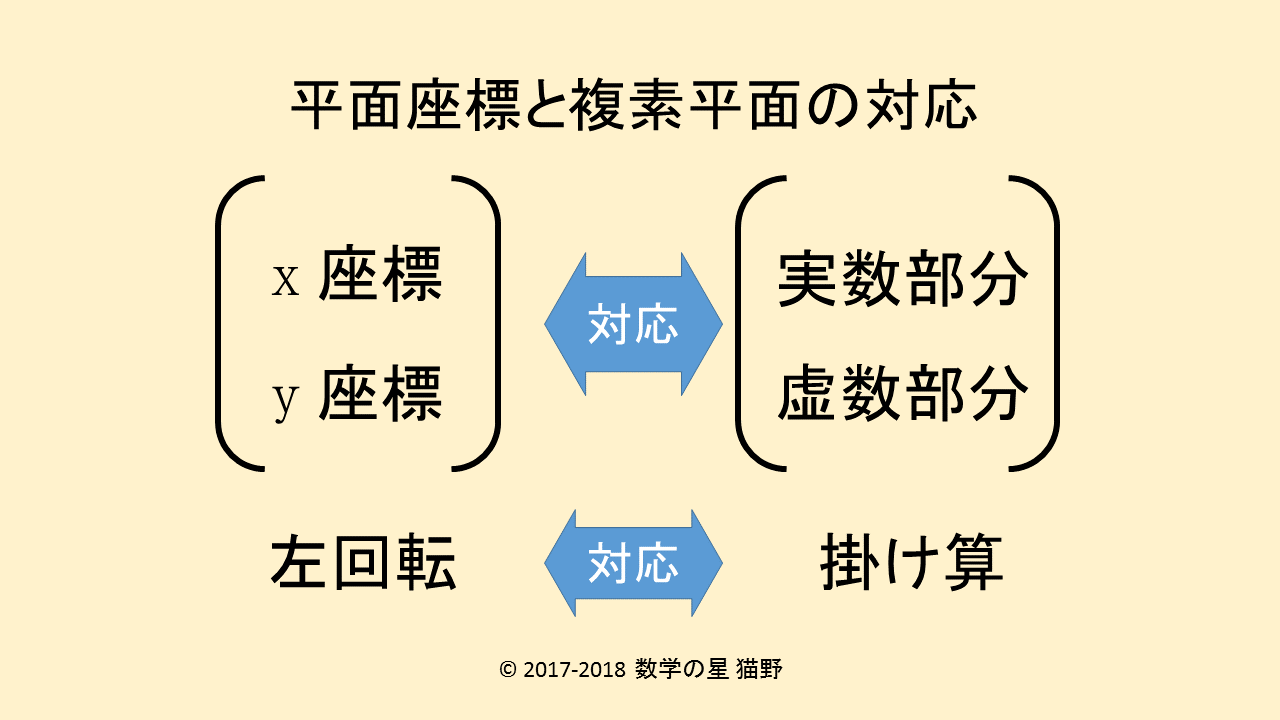 代数
代数