 猫野の微分積分
猫野の微分積分 微分可能とは限らない合成関数の微分係数を求める問題
問題\(g(x)\)は連続関数(微分可能でとは限らない)で\(g(0)=1\)とする。\(\displaystyle f(x)=\frac{x}{g(x)+2}\)とするとき、\(f^{\prime}(0)\)を求めよ。解答(解き方)\(x...
 猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分 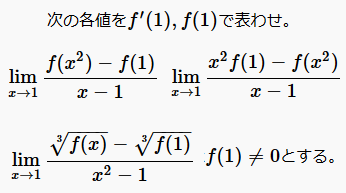 猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分  猫野の微分積分
猫野の微分積分