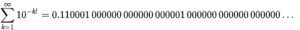\( 0.999 \cdots \)の意味にについて、やはり書いてみたい。
\( 0.999 \cdots \)は、私の好きな級数である。
もちろん、$$ 0.999 \cdots \underset{\mathrm{def}}{=} \sum_{k=1}^{∞} \frac{9}{10^k} $$で定義する。無限級数の和の意味であるから、これは収束して、
\( 0.999 \cdots =1 \)という等式が成立する。
いや、これはこれでよいのである。
それにしても、なぜ論争となるのか考えた。それは\( 0.999 \cdots =1 \)の定義があやふやななかで議論しているからであろう。式の定義を異なって解釈している両者が自己主張しあっている局面がよくみられる。定義があやふやなことに気がつかないで議論している場合も多い。そういう私も、この式の意味について何度も考えさせられ、そして無限の不可思議を味わっているのである。自分自身で論争している。
ここでは、式が正しいとか正しくないとかの結論をだすことではなく、なぜ論争となるかに注目するのである。やはり、普通に数を学んだ(中高ぐらいのレベル)であれば、この等式は直感に反するのである。いろんな証明をみせられても、そこにはなんらかのアキレスと亀のようなパラドックスが隠れていると思ってしまう。
実数とはなにか、定義できるようになるともっと奥深さを味わうことができるかもしれない。定義できな場合は、通常、実数というのを無限小数として認識する。実数を小数表示(つまりは級数表現)で表して理解する。しかし、同じ数に対して2つの無限小数(有限小数も0が無限い続いていると考えてここでは無限小数と表記する。つまり\(1=1.000\cdots\)と考える。)として表わされることは、許したくないのだ。暗に、異なった無限小数は異なる実数を表すのが習慣や経験から得られる事実なのだ。しかし、9の循環は違った。9が循環する小数はどこかかしらで繰り上がって0の循環となるのである。この直感に反するこれはどこに起因するものなのか。直感には反するが、どうも\( 0.999 \cdots =1 \)と結論付けざるを得ない。そして、大学生までは、私も誇らしげに、\( 0.999 \cdots =1 \)を説いていた。
しかし、あるとき、数学セミナーという雑誌で、\( 0.999 \cdots \ne 1 \)となる数の体系もある、と簡単なコメントがある記事をみた。詳細は書かれていなかった(おそらくだが、それは超実数を示唆していたように思う)。それからである、今の実数を鵜呑みに信じることは浅はかなことだと思った、そして、数の世界はもっと広がるのだと確信した。
実は、心のどこかで\( 0.999 \cdots \ne 1 \)でもよいのではないかと、思っていたのだ。\(ε=1-0.999\cdots\)とおいて新しい数ができるのではないかと考えたりもした。
しかし残念ながら、\( 0.999 \cdots \ne 1 \)となる数体系には出会っていない。いまだ、結論が得られず、このようなサイトで思いをぶち上げてる。