こんな論文「素数の分布はベンフォードの法則に従っている」がありました。
これがどんな意味を持っているのか?その意味がどうにも腑におちなくて、自分でも検証してみました。
素数はいろんな意味でランダムに出現していると言われていますが、先頭の数がどのような分布になっているのか考えてみたのです。
素数定理
[ad#top]
有名な素数定理によって、素数がどのように出現するのかある程度はわかります。
ウィキペディアによる素数定理を参照すれば素数定理については詳しくわかります。
ここでも、慣例にしたがって、x 以下の素数の個数を表す素数関数をπ(x)で表します。
さらにここでは、素数関数を2変数に拡張して、x以下でかつyより大きい範囲での素数の個数を表す関数をπ(y,x)で表すことにします。
すなわち、
\(π(y,x):=π(x)-π(y)\)
¥(π(x)=π(1,x)¥)
です。
素数の最高位の数の分布
10未満の場合の素数分布
つまらない例になりますが、10以下の素数は、2,3,5,7の4つで、最高位の数もそれぞれ2,3,5,7となります。
したがって、分布は
| 1で始まる | 2で始まる | 3で始まる | 4で始まる | 5で始まる | 6で始まる | 7で始まる | 8で始まる | 9で始まる | |
| 10未満の素数の個数 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
こうなります。
100未満の場合の素数分布
| 1で始まる | 2で始まる | 3で始まる | 4で始まる | 5で始まる | 6で始まる | 7で始まる | 8で始まる | 9で始まる | |
| 10未満の素数の個数 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 10~99までの素数の個数 | 4 | 2 | 2 | 3 | 2 | 2 | 3 | 2 | 1 |
| 100未満の素数の個数 | 4 | 3 | 3 | 3 | 3 | 2 | 4 | 2 | 1 |
あとあとのことを考えて、10~99の個数を列挙して合計として100未満の個数を表にしました。
1000未満の場合の素数分布
| 1で始まる | 2で始まる | 3で始まる | 4で始まる | 5で始まる | 6で始まる | 7で始まる | 8で始まる | 9で始まる | |
| 10未満の素数の個数 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 10~99までの素数の個数 | 4 | 2 | 2 | 3 | 2 | 2 | 3 | 2 | 1 |
| 100~999までの素数の個数 | 21 | 16 | 16 | 17 | 14 | 16 | 14 | 15 | 14 |
| 1000未満の素数の個数 | 25 | 19 | 19 | 20 | 17 | 18 | 18 | 17 | 15 |
10000未満の場合の素数分布
| 1で始まる | 2で始まる | 3で始まる | 4で始まる | 5で始まる | 6で始まる | 7で始まる | 8で始まる | 9で始まる | |
| 10未満の素数の個数 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 10~99までの素数の個数 | 4 | 2 | 2 | 3 | 2 | 2 | 3 | 2 | 1 |
| 100~999までの素数の個数 | 21 | 16 | 16 | 17 | 14 | 16 | 14 | 15 | 14 |
| 1000~9999までの素数の個数 | π(1000, 2000) |
π(2000, 3000) |
π(3000, 4000) |
π(4000, 5000) |
π(5000, 6000) |
π(6000, 7000) |
π(7000, 8000) |
π(8000, 9000) |
π(9000, 10000) |
| 10000未満の素数の個数 | 160 | 146 | 139 | 139 | 131 | 135 | 125 | 127 | 127 |
こんどは、素数の個数をあらわすπ(y,x)を使って表を作りました。π(1000,2000)は正確にはπ(1000,1999)とすべきところですが、2000は素数でないのでπ(1000,2000)=π(1000,1999)です。ですから見やすさを表現するためにわざとπ(1000,2000)と記載しています。
1で始まる素数が多くなる傾向がみえてきました。
105未満の場合の素数分布
| 1で始まる | 2で始まる | 3で始まる | 4で始まる | 5で始まる | 6で始まる | 7で始まる | 8で始まる | 9で始まる | |
| 10未満の素数の個数 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 10~102までの素数の個数 | π(10, 2*10) |
π(2*10, 3*10) |
π(3*10, 4*10) |
π(4*10, 5*10) |
π(5*10, 6*10) |
π(6*10, 7*10) |
π(7*10, 8*10) |
π(8*10, 9*10) |
π(9*10, 102) |
| 102~103までの素数の個数 | π(102, 2*102) |
π(2*102, 3*102) |
π(3*102, 4*102) |
π(4*102, 5*102) |
π(5*102, 6*102) |
π(6*102, 7*102) |
π(7*102, 8*102) |
π(8*102, 9*102) |
π(9*102, 103) |
| 103~104までの素数の個数 | π(103, 2*103) |
π(2*103, 3*103) |
π(3*103, 4*103) |
π(4*103, 5*103) |
π(5*103, 6*103) |
π(6*103, 7*103) |
π(7*103, 8*103) |
π(8*103, 9*103) |
π(9*103, 104) |
| 104~105までの素数の個数 | π(104, 2*104) |
π(2*104, 3*104) |
π(3*104, 4*104) |
π(4*104, 5*104) |
π(5*104, 6*104) |
π(6*104, 7*104) |
π(7*104, 8*104) |
π(8*104, 9*104) |
π(9*104, 105) |
| 100000未満の素数の個数 | 1193 | 1129 | 1097 | 1069 | 1055 | 1013 | 1027 | 1003 | 1006 |
この表から計算の方針がわかってきます。
例えば、1~105の範囲で1で始まる素数は、
π(1,10)+π(10,2*10)+π(102,2*102)+π(103,2*103)+π(104,2*104)
で計算すればよいことがわかります。これをπ(105)で割れば、1で始まる素数の出現率となります。
また、π(x)については、x/log(x)で近似してみます。
これで計算すると、100000未満の素数で1から始まる近似された個数は、1070でした。
この近似式で1で始まる素数の出現率は、1070/8686=12.3%
\[ \frac{\sum_{k=1}^{n} π(10^k,2*10^k)}{π(10^{n+1})} \]
こでれ、nを∞にしたときの極限をもとめたら、1から始まる素数の出現率になるはずですが、ものすごく収束がわるいようで30%になりそうではありませんでした。
下記が実際にEXCELで計算した結果です。
| 先頭が1 | 先頭が2 | 先頭が3 | 先頭が4 | 先頭が5 | 先頭が6 | 先頭が7 | 先頭が8 | 先頭が9 |
| 13.43% | 12.34% | 11.65% | 11.15% | 10.78% | 10.49% | 10.25% | 10.04% | 9.87% |
| 13.08% | 12.10% | 11.53% | 11.13% | 10.83% | 10.60% | 10.40% | 10.24% | 10.09% |
| 12.64% | 11.89% | 11.44% | 11.13% | 10.90% | 10.71% | 10.55% | 10.42% | 10.31% |
| 12.33% | 11.74% | 11.39% | 11.14% | 10.95% | 10.79% | 10.66% | 10.55% | 10.46% |
| 12.12% | 11.64% | 11.34% | 11.14% | 10.98% | 10.85% | 10.74% | 10.64% | 10.56% |
| 11.97% | 11.56% | 11.31% | 11.14% | 11.00% | 10.89% | 10.79% | 10.71% | 10.64% |
| 11.85% | 11.50% | 11.29% | 11.13% | 11.01% | 10.91% | 10.83% | 10.76% | 10.70% |
| 11.77% | 11.46% | 11.27% | 11.13% | 11.03% | 10.94% | 10.86% | 10.80% | 10.74% |
| 11.70% | 11.43% | 11.25% | 11.13% | 11.03% | 10.96% | 10.89% | 10.83% | 10.78% |
| 11.64% | 11.40% | 11.24% | 11.13% | 11.04% | 10.97% | 10.91% | 10.86% | 10.81% |
| 11.60% | 11.37% | 11.23% | 11.13% | 11.05% | 10.98% | 10.93% | 10.88% | 10.83% |
| 11.56% | 11.35% | 11.22% | 11.13% | 11.05% | 10.99% | 10.94% | 10.90% | 10.86% |
| 11.53% | 11.34% | 11.21% | 11.13% | 11.06% | 11.00% | 10.95% | 10.91% | 10.87% |
| 11.50% | 11.32% | 11.21% | 11.13% | 11.06% | 11.01% | 10.96% | 10.92% | 10.89% |
| 11.47% | 11.31% | 11.20% | 11.13% | 11.06% | 11.01% | 10.97% | 10.94% | 10.90% |
| 11.45% | 11.30% | 11.20% | 11.12% | 11.07% | 11.02% | 10.98% | 10.95% | 10.92% |
| 11.43% | 11.29% | 11.19% | 11.12% | 11.07% | 11.03% | 10.99% | 10.96% | 10.93% |
| 11.42% | 11.28% | 11.19% | 11.12% | 11.07% | 11.03% | 10.99% | 10.96% | 10.94% |
| 11.40% | 11.27% | 11.18% | 11.12% | 11.07% | 11.03% | 11.00% | 10.97% | 10.94% |
| 11.39% | 11.26% | 11.18% | 11.12% | 11.08% | 11.04% | 11.01% | 10.98% | 10.95% |
| 11.37% | 11.25% | 11.18% | 11.12% | 11.08% | 11.04% | 11.01% | 10.98% | 10.96% |
| 11.36% | 11.25% | 11.17% | 11.12% | 11.08% | 11.04% | 11.01% | 10.99% | 10.97% |
| 11.35% | 11.24% | 11.17% | 11.12% | 11.08% | 11.05% | 11.02% | 10.99% | 10.97% |
| 11.34% | 11.24% | 11.17% | 11.12% | 11.08% | 11.05% | 11.02% | 11.00% | 10.98% |
| 11.33% | 11.23% | 11.17% | 11.12% | 11.08% | 11.05% | 11.03% | 11.00% | 10.98% |
| 11.32% | 11.23% | 11.17% | 11.12% | 11.08% | 11.05% | 11.03% | 11.01% | 10.99% |
| 11.32% | 11.22% | 11.16% | 11.12% | 11.09% | 11.06% | 11.03% | 11.01% | 10.99% |
| 11.31% | 11.22% | 11.16% | 11.12% | 11.09% | 11.06% | 11.03% | 11.01% | 11.00% |
| 11.30% | 11.22% | 11.16% | 11.12% | 11.09% | 11.06% | 11.04% | 11.02% | 11.00% |
| 11.30% | 11.21% | 11.16% | 11.12% | 11.09% | 11.06% | 11.04% | 11.02% | 11.00% |
この表をグラフにするとよくわかるのですが、だんだん差が縮まっていき、最終的には全部1/9に収束しそうな形です。
集計のしかたに問題があるのでしょうか?
EXCELのグラフなのでちょっと見出しの説明をします。
系列1は、1で始まる素数の個数のラインで、横軸の1,2,3,・・・は、102,103,104,・・・で1030 までの範囲まで計算したことを示します。
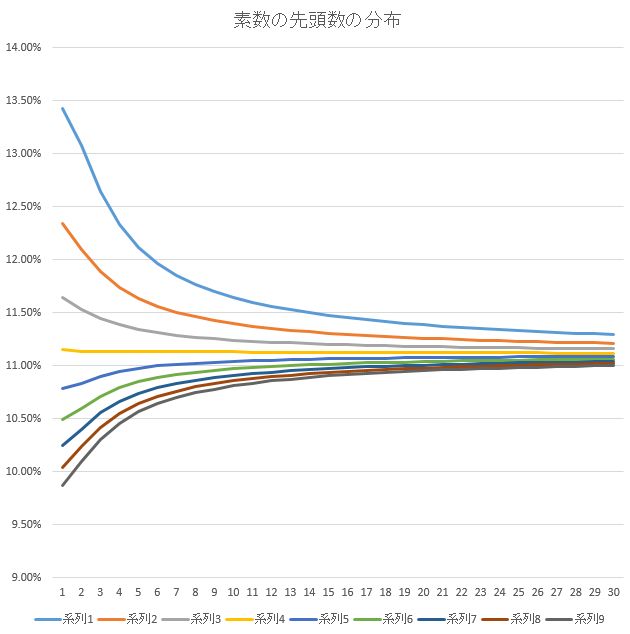
この計算方法からで推測しますと、最初の方こそ偏りがありますが、範囲を広げていくに連れ、素数の先頭の数の出現率はだんだんと1/9≒11.11%に均一に近づいていくように思われます。
※EXCELで扱える数の限界10300まで計算してみましたが、やはり、それぞれの出現率はますます11.11%に近づいていました。
結論
n以下の素数の分布を考え、n→∞にしたときの極限から考えた素数分布
おそらく、素数の先頭の数の出現率は、どの数であっても1/9に収束する。
素数の個数関数を近似式 π(x):=x/log(x) で近似した場合の話になりますが、どの近似式を使っても、同様の結果になると思います。
実際に検証した結果、論文の内容と異なる結果になってしまいました。
意に反した結果となり困惑です。
あの論文「素数の分布はベンフォードの法則に従っている」は一体!?
自分なりの結論ですが、素数はやはりベンフォードの法則のような偏りがあるのではなく一様に分布(大きくなっていくにつれ密度は薄くなっていきますが)していると考えられます。
ディリクレの級数定理もそれを物語っていると考えます。
予測
[ad#foot]
ただ、自然に分布している数のうち、素数であるものだけを抜き出すとこれはベンフォードの法則に従っているのではないかと思います。
つまり、ベンフォードの法則が成立している数の分布があった時、そこから素数だけを抜き出す(フィルタリングする)と、その素数の出現率はベンフォードの法則に則っているということです。これなら納得できます。
[ad#foot]
