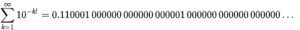多重完全数とは
[ad#top]
もとの数の約数の和が、もとの数の倍数になる自然数のことをいいます。k倍になっているとき、kを明示的に示すため、k倍完全数とも呼ばれています。
これは、約数の逆数の和が整数kになっている自然数とも言えます。

プライムナンバーズ ―魅惑的で楽しい素数の事典 (O’Reilly math series)
すぐにわかりますが、素数は完全数になりえません。合成数であればあるほど、約数の和はもとの数より大きくなっていきます。
(多重)完全数を探すことを考えたとき、既知の完全数を素因数分解すると、当然それは合成数ですが、現れてくる素因数は独特の形式になっています。
コンピューターで完全数を探す時、数値をインクリメントしながら探していくよりも素因数を絞って探したほうが効率的かもしれません。
(もれなく探す場合は、やはり総当りで確認するにことたことはないです。)
既知のk倍完全数を素因数分解してみます。
2倍完全数:
6=2*3
3倍完全数:
120=23*3*5
672=25*3*7
523776=29*3*11*31
459818240=28*5*7 19*37*73
1476304896=213*3*11*43*127
51001180160= 214*5*7*19*31*151
4倍完全数:30240=25*33*5*7
5倍完全数:14182439040=27*34*5*7*112*17*19
6倍完全数:154345556085770649600=215*35*52*72*11*13*17*19*31*43*257
素因数2の出現率が高く、指数部分をみると、1が多いです。
しかし、2以外の素因数であっても、指数部分に2や3がでてくることもあり、大きな数になってくれば指数部分も増えていくことは予想されます。
とりわけ、よく問題されるのは、偶数か奇数かです。奇数の完全数は発見されていません。
上記の素因数分解をみると、どれも素因数2を大量に含んでいます。
これをみたら、奇数の完全数はないだろうと思わざるを得ません。が一方、計算されている数があまりにも小さすぎるためだとも思えます。
素因数が2個の完全数
[ad#foot]
現在のところ、完全数に関する定理で最も美しい成果は、2000年以上も前のメルセンヌ素数に関する下記の定理でしょう。
2n-1が素数 → 2n-1(2n-1)は完全数である。
偶数の完全数 → 2n-1(2n-1)の形である。
これは、2と2n-1の形の素数からできる完全数です。
nがどういったときに、2n-1が素数になるのかという問題を孕んでいますが、必要十分条件であることがなによりも画期的な命題です。