[msg#wsiki]
問題
aは正の数、
p,qはp>qの正の整数、
\(\displaystyle a_1=1\)
\(\displaystyle a_n^p a_{n-1}^q=a\) \((n≧2)\)
をみたす正数列を{an}とする。
このとき、
\(\displaystyle \lim_{n\rightarrow \infty} a_n\)を求めよ。
(名大)
こんな問題です。
解き方
ひらめきが必要です。
この問題では対数をとって漸化式を別の形にします。
\(p \log(a_n)+q \log(a_{n-1})=\log a\)
\(b_n=\log a_n\)
\(b=\log a\)
とおくと、
\(\displaystyle pb_n +q b_{n-1}=b\)
\(\displaystyle b_n=-\frac{q}{p}b_{n-1}+\frac{b}{p}\)
aが正、anが正というのが効いています。
よくある漸化式(隣接二項間漸化式)の数列{bn}なので一般項が求められます。
ここまでくれば、anの極限を求めるの見通しができあがります。
bnの一般項が求められるので、bnの極限から答えが得られます。
解答
\(b_n=\log a_n\)
\(b=\log a\)
とおくと、
\(\displaystyle pb_n +q b_{n-1}=b\)
\(\displaystyle b_n=-\frac{q}{p}b_{n-1}+\frac{b}{p}\)
\(\displaystyle b_n-\frac{b}{p+q}=-\frac{q}{p}(b_{n-1}-\frac{b}{p+q})\)
|-q/p|<1であるからbnは\(\frac{b}{p+q}\)に収束する。
したがって、
\(a_n=\mathbb{e}^{b_n}\) は
\(\displaystyle \mathbb{e}^{b/(p+q)}\)
\(\displaystyle =a^{1/(p+q)}\)に収束する。
答え
\(\displaystyle \lim_{n\rightarrow \infty} a_n =a^{\frac{1}{p+q}}\)
他の数列の極限に関する問題:数列の極限の問題一覧
[ad#foot]
補足
\(a_n\)が\(\alpha\)に収束すると仮定すると、
anpan-1q=a
の両辺の極限をとることができて、
\(\alpha ^p \alpha ^q=a\)
となりますから、
\(\displaystyle \alpha=a^{1/(p+q)}\)
を得ます。
しかし、このやり方は、\(\alpha\)に収束するという前提があるからできるのであって、問題から収束するかしないかを調べるためには、上記のbnの形を導くことが必要です。
猫野の解析は

鉄則微分・積分
をテキストとして使っています。
鉄則ゼミ3の問題を解いています。
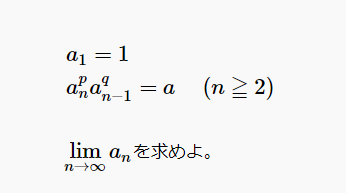




コメント