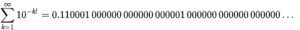簡単にいうと
稠密(ちゅうみつ)とは、たくさん集まっているということで、一番わかりやすい例が「有理数(全体の集合)です。連続は稠密よりもさらにたくさん集まっているというこおとで、一番わかりやすい例が実数(全体の集合)です。実数も稠密ですが、有理数は連続でないというのがポイントです。
ここで言っている「たくさん」というのは、もちろん無限です。
さて、稠密と連続が異なる概念であるというのは、有理数と実数の例で説明されるのですが、その違いはいったいどこにあるのでしょうか。
連続(完備)
連続関数、連続写像、実数の連続性など数学用語で連続という概念がよく出てきます。
一番身近な例は、連続関数で解析などでよく使われます。
基礎的には、実数の連続性があって、幾何学的に一般化すると連続写像、解析的に具体化すると連続関数といった具合に展開されますが、連続の概念のベースにあるのは、実数の連続性です。
実数の連続性は完備性と言われることもあります。連続というより、完備といったほうが変な先入観がなくてよいかもしれません。完備というのは、なにかが完成されたということで、逆に考えると稠密とはなにか欠けている可能性があるということになります。
実数はなにが完成しているのかといえば、コーシー列が必ず収束するということです。つまり有理数に収束しないコーシー列が存在するから有理数は完備でない、連続でないというわけです。
わかりきったことですが、有理数を完備化したものが実数といってもよいです。実数の最大の特徴でしょう。実数は有理数の不完全な部分をすべて備えた存在なわけです。
この当たりは広く知れ渡っていることで、解析の本を読めばもっと詳しく、正確に説明されています。
稠密な集合は完備な集合の部分集合
ここで、すぐにわかることですが、稠密というのはなんらかの部分集合であるということです。完備化という、不完全な部分を補うことで、稠密な集合は完備化された集合の部分集合となります(みなせせます)。
有理数が稠密と言いましたが、これは有理数が実数の部分集合と考えていることに他なりません。逆の視点でみると、ある意味、有理数を拡大して実数ができたとみなすことができます。
完備化というのは、拡大することを意味します。
それでは、実数も稠密なんで完備化を行うことができるはずです。実数を完備化したら実数を拡大することになるわけですが、それはどのような集合になるのでしょう。
結論をいうと、実数を完備化しても実数のままです。実数は完備化によってこれ以上拡大できないということになります。
実数はもう拡大できないのか
いままでは、一般論です。前置きが非常に長くなってしまいました。
ここからが研究です。実数はもう拡大できないのでしょうか。答えは「できます!」となります。ここからは、研究領域ですから、まだ一般の教科書には載っていません。整備が行き届いていないのです。
実数の完備化は、コーシー列が収束するように備えられました。「コーシー列が収束する」を別の条件に変えることで、別の完備化が可能になるのです。さて、コーシー列に変わる条件としてなにがあるのでしょうか。
別のタイプの完備化によって、実数をさらに拡大することを考えていますが、それは第二弾の記事としたいと思います。
[ad#foot]