代数 2009年一橋大学タクシー数を求める問題
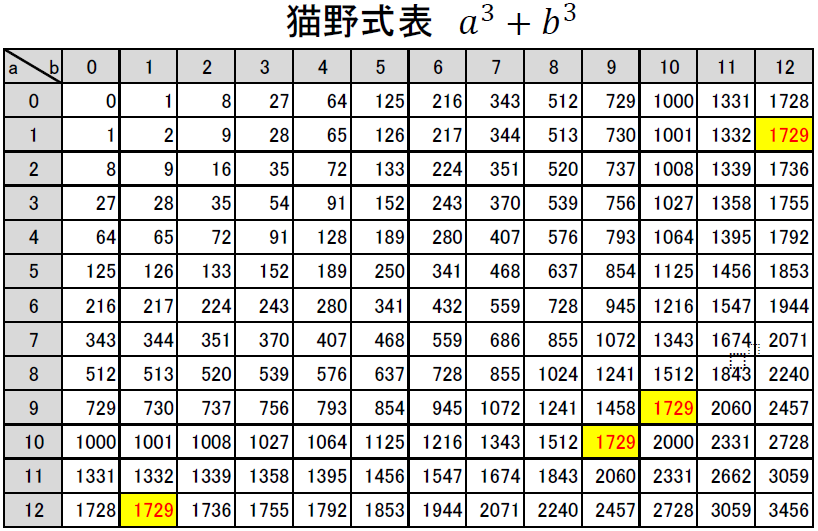
タクシー数に関する入試問題問題２以上の整数n,mは、\(n^3+1=m^3+10^3\)を満たす。m,nを求めよ。(２００９年の一橋大学前期の数学問題より)解答例整数に関する不定方程式です。素因数分解し、有限個の分解によって場合分けし解を絞...
数論
代数 代数 天才数学者ラマヌジャンのタクシー数の研究
ラマヌジャンがあるタクシーのナンバーに書かれていた１７２９をみて、それは、「２つの３乗数の和として２通りに表すことができる最小の自然数」と言ったことがタクシー数の発端です。ラマヌジャンは、「インドの魔術師」とも呼ばれた天才数学者で、その才能...
数論 複雑な２次の因数分解でもたすき掛け不要！
たすき掛けで因数分解したくても、適した数が見つからない！２次の因数分解の話ですが、「たすき掛けで因数分解できない！」こんなことありませんか？たすき掛けのやり方は習って知っている、でも、答えが見つからない！例えば、\(6x^2-11x+4\)...
代数 平方根(ルート)の近似値を計算する方法
√iなどの複素数の平方根については、「複素数の平方根を求める公式と使用例」を参照ください。√２を求めよ√２は無理数ですので、√2を実数(小数表示)で表すと、1.4142・・・と無限小数となります。この、無理数√2の1.4142・・・はどうや...
代数 複素数の平方根(ルート)を求める公式と使用例
数式の展開に時間がかかります。ご容赦ください。先に、結論となる公式を書いておきます。b≧0の時\(\displaystyle \sqrt{a+bi}\\=\pm \left( \sqrt{\frac{a + \sqrt{a^2+b^2}}...
代数 注意！二次方程式の解の公式が使えない
2次方程式の解の公式\(ax^2+bx+c=0,(a \ne 0)\)という\(x\)に関する2次方程式の解\(x\)は、\で与えられる。というのが解の公式と呼ばれるものです。式の形を覚えるのに苦労しますが、完全に覚え使いこなせるようになる...
代数 算数からはじまる素数
素数との出会い小学校の５年生のときに素数をならった覚えがあります。その時の授業はかなり印象的でした。今振り返ると、考える授業といってもよいと思う授業でした。不思議だったのです。５年のあるとき、先生が突然素数をもとめる授業を行ったのです。素数...
数論 円周率の日に円周率の計算
３月１４日は？ホワイトデー！、それよりも重要な日、円周率の日です！本日は円周率の日円周率の計算方法は他数あれど、有名なのは、arctan()を使う方法（その中でも特にマチンの公式）。しかし、それよりも単純で、効率的な方法が。その名は、ガウス...
代数 サンダラムを改良して素数を求める
エラトステネスの篩を改良したサンダラムの篩によって素数を効率よく求めることができました。さらなる改良は可能かサンダラムの篩をさらに改良することはできるでしょうか？原理としては可能です。どのように改良すればよいのか、それはサンダラムのふるいが...
不等式 本当に「1=0.999…」でよいのか？
実数の定義もままならないのに、「1=0.999…」を主張する人がたくさんいます。よくある「1=0.999…」の証明その１\(0.333...＝\frac{1}{3}\)である。両辺を３倍する。\(0.333...*3=\frac{1}{3}...