ピタゴラス数とは
三平方の定理(ピタゴラスの定理)にでてくるあの式です。自然数の組の場合、ピタゴラス数と呼ばれます。
三平方の定理(ピタゴラスの定理)とは、「直角三角形の3辺の長さをそれぞれa,b,c(斜辺)としたとき、\(a^2+b^2=c^2\)の関係がある。」という定理です。逆も成立しています。すなわち「\(a^2+b^2=c^2\)の関係がある\(a,b,c\)の辺の長さを持つ三角形は、直角三角形である。」が成立します。
\(a^2+b^2=c^2\)の関係式を満たす自然数\(a,b,c\)の組み合わせをピタゴラス数と呼びます。一番有名なピタゴラス数は、(3,4,5)です。
\(3^2+4^2=5^2\)になっていますね。
その他、 (5, 12, 13)や、(6,8,10)などがありますが、どのような自然数の組み合わせがピタゴラス数になっているのかかなり昔から知られていて、実は全てのピタゴラス数を表す式もあるのです。
すぐにわかるのは、(a,b,c)がピタゴラス数なら、自然数\(n\)に対して、(na,nb,nc)もピタゴラス数になっています。逆に、(a,b,c)がピタゴラス数で、その公約数としてpがあった時、(a/p,b/p,c/p)もピタゴラス数になります。
証明はいたって簡単で、\(a^2+b^2=c^2\)の両辺に\(n^2\)をかけたり、\(p^2\)で割ったりすれば示せます。
ここでは、やり方として一番簡単であろう円の方程式を使って求めてみます。簡単というのは、約数がどうのこうのなどを考えず、式をたてて計算していけば求められるという意味です。
なお、bが奇素数であるときの解は入試問題にもなっていて、わりと簡単に求められます。
円の方程式とは
方程式、\(x^2+y^2=r^2\)を満たす実数の組(x,y)をx-y平面座標にプロットすると、原点を中心とした半径rの円ができます。距離の公式からこれがわかります。
特に、\(r=1\)の場合は、単位円と呼ばれてよく使われます。ちなみに、単位円上の点の座標は実数θを使って、\((\cos(θ),\sin(θ))\)で表すことができます。このθは媒介変数と呼ばれ、媒介変数と点を対応させることができています。実はこの例のθは角度になっているので、幾何学的な意味もわかるかなり便利な媒介変数です。
ピタゴラス数を求めるために、これらの幾何学的な知識を使うのですが、私はこの方法がかなり気に入っています。
考え方は、、(a,b,c)がピタゴラス数なら、、\((a/c)^2+(b/c)^2=1\)であるので、(a/c,b/c)は単位円上にあるということです。逆に単位円上にある有理数の座標を持つ点から、ピタゴラス数を見つけることができます。
ピタゴラス数を求める
やり方は、単位円上の座標を媒介変数mを使って表します。mは直線y=mx-1の傾きです。単位円と直線y=mx-1は2点で交わることがわかります。その一つは、(0,-1)です。もう一つの交点を方程式を解いて求めます。
1次式と2次式(単位円)の交点を求めることになるのですが、二つある交点のうち、一つはすでにわかっている点(0,-1)なので、これからう一つの点も特別なことをすることなく求めることができます。というか、交点の座標が求められるように直線の式を選んでいたのでした。
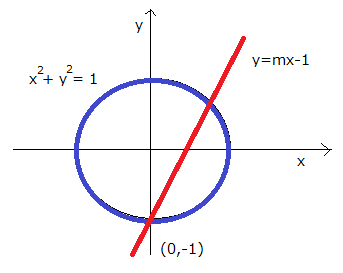
単位円と直線の交点を求める
それでは、連立させて交点を求めます。
\(x^2+y^2=1\)に\(y=mx-1\)を代入します。
\(x^2+(mx-1)^2=1\)
\(x^2+m^2x^2-2mx+1=1\)
\(((1+m^2)x-2mx)x=0\)
よって、交点の座標は、(0,-1)と
\[\left(\frac{2m}{1+m^2},\frac{m^2-1}{1+m^2}\right)\]が求まりました。
やったー!もう一息です。
mが有理数の場合を考えます。すなわち、\(m=p/q (p,qは整数でq\ne0)\)とすると、交点の座標は、
\[\left(\frac{2(p/q)}{1+(p/q)^2},\frac{(p/q)^2-1}{1+(p/q)^2}\right)\]
整理して、
\[\left(\frac{2pq}{p^2+q^2},\frac{p^2-1}{p^2+q^2}\right)\]
これが単位円上の有理数点(座標が全て有理数となっている点)を表しています。
厳密証明するためには、もうちょっと補足や但し書きが必要となりますが、骨格の部分はこれで全て完了です。
さて、この有理数点からピタゴラス数を実際に書き表してみます。
上記座標は単位円上の点を表しているので、
\[\left(\frac{2pq}{p^2+q^2}+\frac{p^2-q^2}{p^2+q^2}\right)=1\]
\[(2pq)^2+(p^2-q^2)^2=(p^2+q^2)^2\]
つまり、\((2pq,p^2-q^2,p^2+q^2)\)がピタゴラス数となります。
符号の問題なども考慮すると、m>1の時にx座標、y座標が共に正となるので、
\[(2pq,p^2-q^2,p^2+q^2)\]ただし、\(p,qはp \gt q \gt 0\)の整数。
でピタゴラス数を表すことができます。
[ad#foot]※コメント1:後の祭りですが固定点を(0,-1)よりも、(-1,0)にしたほうが感じが良さそうでした。まあ、どの固定点をつかっても求める結果は同じなのでこれでよいです。失敗例も勉強になるでしょうから、このまま掲載します。
※コメント2:(a,b,c)がピタゴラス数なら(b,a,c)もピタゴラス数であるのは明らかなので、
\[(p^2-q^2,2pq,p^2+q^2)\]ただし、\(p,qはp \gt q \gt 0\)の整数
と書いても同じことです。こっちのほうが感じがいいです。
※コメント3:一番簡単なピラゴラス数は、p=2,q=1の時になりますが、この値を上の式にあてはめると(4-1,2*2*1,4+1)=(3,4,5)となって、有名なピタゴラス数が求まりました。

コメント
>問題 投稿者:壊れた扉 投稿日:2018年 9月17日(月)07時56分5秒
問題
\(a^2+b^2=c^2\)となる正の実数a,b,cでは、\(a^3+b^3\lt c^3\)となる事を証明せよ。
余裕がある人は2通り作って下さい。
挑戦して一通りは思いつきました。
\(\displaystyle a^2+b^2=c^2\)から、
\(\displaystyle a\lt c,b\lt c \)である。
\(\displaystyle a^3+b^3\lt a^2c+b^2c=(a^2+b^2)c=c^2 c \)
\(x=a/c,y=b/c\)
と置くと、
\(0\lt x,y\lt 1\)
となりますから、
\(0\lt x^3\lt x^2\lt x\lt 1\)
\(0\lt y^3\lt y^2\lt y\lt 1\)
となって、辺々加えて
\(0\lt x^3+y^3\lt x^2+y^2=1\lt x+y<2\)
もとの変数に戻すと、
\(a^3+b^3\lt c^3\)
\(c\lt a+b\lt 2c\)
が得られます。
算数好き(数学はズブの素人)のヒマ老人です。この問題の解全く手が出ません。しかし、死ぬまでには解いてみたく思います。長生きする目的ができ、感謝です。
ところで、私は「gontanoe」なるブログで、素人向けの算数パズルを投稿しています。もしよかったら、のぞいてみて下さい。リンク番号は怪しまれると思い載せませんが、gontanoeで検索で出ます。今、夢中になってるのは、いろいろありますが、nm(m^2-n^2)[m>nで互いに素の自然数]が6の倍数なる事を、小学生レベルの方法で説明でき感動しています。これからよろしくお願い致します。
● x^2+y^2-z^2=0 を満たす自然数の組 (x,y,z) をピタゴラス数
またはピタゴラスの三つ組数 (Pythagorean triple) という
の 模倣犯 に なり果て;
『↓ こんな 模倣犯 に 誰がした』
■ S; 9 x^2+44 x y-12 x z-24 y^2+4 y z+4 z^2=0
を満たす自然数の組 (x,y,z) を媚多娯裸棲(ビタゴラス) 数
または媚多娯裸棲の三つ組数 (ビタゴラス triple) と 定義する!。
●「m,nを任意の二つの整数とするときx=m^2-n^2,y=2*m*n,z=m^2+n^2
が その〇一般的な形〇である」
(完成した際の題名は『こんな女に誰がした』であった[1]。
>GHQから「日本人の反米感情を煽るおそれがある」とクレームがつき、
>題名を『星の流れに』と変更して発売となった[1]。
https://www.youtube.com/watch?v=YmmwcUi3p8M&list=RDYmmwcUi3p8M&start_radio=1#t=7
大阪na___.
https://www.youtube.com/watch?v=Z8JUfGLa54Q&list=RDYmmwcUi3p8M&index=5
http://www.naomiosaka.com/
変数の置き換えをすると、\(X^2+Y^2=Z^2\)
の形になるのでしょうか。