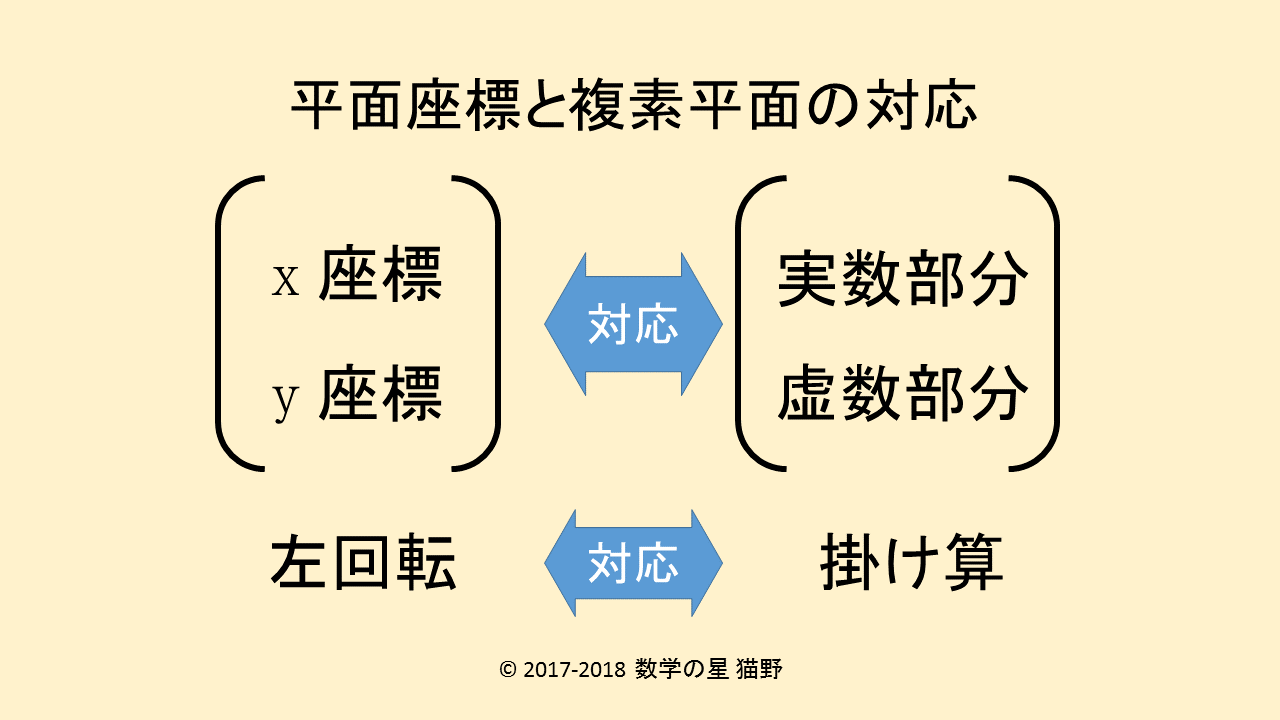
代数 回転行列の代わりにもなる複素数
任意の複素数zは、長さrと偏角tで下記のように表すことができます。\(\displaystyle z=r(\cos t +i \sin t)\)二つの複素数を掛け算すると、長さは長さ通しの積、偏角は和で表される複素数になります。特に長さ1の...
代数 
代数 極座標で複素数のn乗根(累乗根)を求める理由
複素数を、極座標表示するとn乗根が求めやすくなります。極座標表示とは、複素数zを長さrと偏角θで表示する方法です。\(\displaystyle z=x+y i\) \(\displaystyle =r(\cos(θ)+\sin(θ) i)...
代数 複素数と実数、虚数の関係
複素数とは、a+bi (a,bは実数)の形で表すことができる数です。iは虚数単位と呼ばれ、２乗すると-1になる数です。複素数a+biにおいて、aのことを実部（実数部分）、biのことを虚部(虚数部分)と呼びます。ここで、複素数a+biのbがゼ...
数論 複素数に符号を定義すると虚数は符号となる
複素数では正や負の概念がありませんが、符号という概念を拡張すると、複素数にも正や負と似た概念が適用できます。まず実数の符号についての性質をつかい、それに似せて複素数の符号を定義します。複素数の符号の一部として、正や負の概念を複素数に適用する...
数論 数の符号のプラス・マイナスは、足し算・引き算と区別される
実数はゼロを除けば正か負のどちらに分類され、正の実数はプラスの符号「+」、負の実数にはマイナスの符号「-」がつけられます。
代数 複号同順でマイナスプラス記号が使われます
プラスマイナス記号「±」は、、プラス記号「+」とマイナス記号「-」を合わせた記号です。「±」記号は、２次方程式の解の公式でおなじみの記号で、読み方は「プラスマイナス」です。プラスマイナス記号±の使い方これは、符合だけ異なる二つの式を一つにま...
数論 テトレーションなどのハイパー演算子から演算を考える
足し算を繰り返すことで、かけ算が定義でき、かけ算を繰り返すことで、べき乗算が定義できます。この考え方を発展させ、べき乗算を繰り返すことから、新しい演算が定義できます。それがテトレーション（超ベキ算）と呼ばれる演算です。
解析 最強のロピタルの定理でもうっかり使うと答えを間違う問題例
極限を求めるツールとして最強のロピタルの定理ですが、うっかりすると誤用してしまう場合があります。ロピタルの定理には、適用できるための前提条件がいろいろあります。そのほとんどは、それほど神経質になる必要はありません。ただ、一つだけうっかり間違...
猫野の微分積分 半円に内接するある四角形の最大の面積を求めるの問題
問題ABを直径とする半径１の半円周上の動点をP,Qとする。AP=PQを満たす四角形APQBの面積の最大値とそのときのBQの長さを求めよ。解答（解き方）四角形APQBの面積をなんらかのパラメータを使って表し、パラメータがどの値の時に最大値とな...
猫野の微分積分 次数があってsin,cosの扱いが難しい微分の問題
問題関数\(\displaystyle f(x)=3( \sin x - \cos x) + \cos{2x}\)の最大値を求めよ。解答（解き方）\(\sin x と \cos x\)の対称式ではありませんが、すこし工夫すると対称式の問題と...