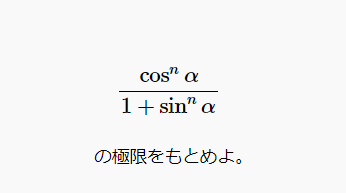猫野の微分積分 数列の極限を求める問題と解き方cos^n(a)/(1+sin^n(a))他
問題(1)数列の極限を求める(三角関数あり)問題\(\displaystyle \frac{\cos^n \alpha}{1+\sin^n \alpha}\)の極限をもとめよ。解き方いきなり三角関数があって面食らいますが、\(\displa...
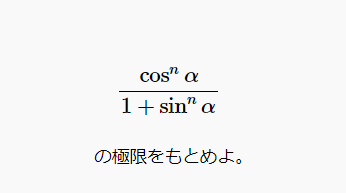猫野の微分積分 
猫野の微分積分 連続関数の定義と合成関数の極限（高校生向け）
連続関数の定義関数f(x)がx=aで連続である関数f(x)が連続とは、\(\displaystyle \lim_{x \rightarrow a} f(x)=f(a)\)のことです。もちろん、これは、\(\displaystyle \lim...
猫野の微分積分 三角関数の基本の極限値
三角関数の極限で基本中の基本の不等式と極限式を示します。三角関数の基本不等式\(\displaystyle 0 \lt \sin{x} \lt x \lt tan{x} \)ただし、0<x<π/2の場合に限ります。ちなみに、-π/2 < x...
猫野の微分積分 関数の極限を求める問題にある落とし穴(x→-∞)
関数の極限を計算するときに、∞は正、ｰ∞は負と考える。わかっているとはいえ、符号の扱いに注意しないと落とし穴に落ちることがある。例題\(\displaystyle \lim_{x \rightarrow -\infty} \frac{\sq...
猫野の微分積分 無限大における関数の極限とその例題
xが無限大になったときの関数の極限も考えることができる。収束する場合もあるし、発散する場合もある。x→∞、x→-∞での関数f(x)の極限パターンx→∞でbに収束する場合xを限りなく増加させたときに、f(x)の値がある実数bに限りなく近づく(...
猫野の微分積分 関数の極限に関する定義と４つの例題
xの関数f(x)と実数aに対し、f(x)はｘ＝aで値をもっていても、もたなくてもよいが、x=aの前後では値が決まっているとする。関数の極限の４パターン関数の極限としては、下記の４パターンある。 極限値がある。 正の無限大に発散する。 負の無...
猫野の微分積分 循環小数は無限等比級数であって有理数である
有限小数と循環小数実数を小数で表すことができるが、小数で表したときの数の並び方で、有限小数、循環小数、無限小数に分類される。例を見たほうが、わかりが早いのでいくつか例を示す。有限小数の例 0.03 0.125 0.99999など 10のベキ...
猫野の微分積分 無限級数は足す順番で収束発散の結果が変わる
足す順番を替えて無限級数の和を求めてみる下記の二つの例でそれを確かめます。（１）数列\(\displaystyle a_n=\frac{n+1}{n}-\frac{n+2}{n+1}\)\(\displaystyle =\frac{1}{n...
猫野の微分積分 無限級数の和の意味で勘違いしやすいところ
無限級数の和の意味でよくある勘違い勘違いを示す前に、無限級数についての定義を書いておきます。無限級数とは無限級数とは、数列{an}が与えられた時に、これを順に＋で結んだ式\のことです。無限級数を\と表します。とく使われてる記号ですから自然に...
集合論 ハムサンドイッチの定理
ハムサンドイッチの定理とは食パン（上）、ハム、食パン（下）からできているサンドイッチを平面で同じ量にカットできるという定理です。実際には細かい誤差は発生するにせよ、サンドイッチを半分にきることなどよくやっていますよね。包丁の位置をちょっと右...