整数論の問題を紹介します。 二つの自然数を素数で割ったときの余りがどのようになっているのかを評価する問題になっています。 問題 \(a,b\)を正の整数とする。どんな素数\(p\)についても\(a\)を\(p\)で割った […]
数論の入門問題はこれから始まる
素数や、約数、倍数などの一通りの知識がついたところで、取り組む数論的な問題を掲示します。 フェルマーの定理から、数論に興味がでてきて、もっと数について詳しく研究したいと思ったはいいものの、なかなかとっかかりが見つからない […]
不等式問題[2006年筑波大前期理系第２問]
問題(2006年筑波大前期理系第２問) \(a \ge b \gt 0, x \ge 0\) とし、\(n\)は自然数とする。次の不等式を示せ。(1) \(\displaystyle 0 \le e^x-(1+x) \l […]
行列の割り算はこうなっている！
行列の計算を習って最初に面食らうのは、交換の法則です。そして、行列計算において最初に立ちはだかる壁は、行列の割り算についてです。 結論からいうと、行列にも割り算を考える事はできます。しかし、普通の数と比べて扱いがとてもシ […]
積分にでてくる∫やdxの記号の意味
積分の式は、\(\displaystyle \int（xの関数）dx\)という形で書かれます。 この\(\int\)と\(dx\)の記号は慣れないとなかなか読み解けないものです。 記号の意味や解釈はいろいろありますが、こ […]
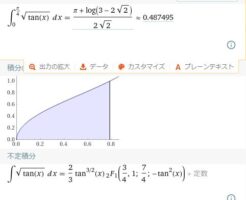
超難問√tan(x)の不定積分と定積分の解き方
関数\(\sqrt{\tan(x)}\)の積分です。 微分と比較にならないほど積分ははるかに難しいです。 まずは、素敵なウルフラムの計算結果を参照してください。 https://www.wolframalpha.com/ […]
超実数のイメージがわくように説明するよ
超実数(Hyperreal Number)について調べていると、超フィルターの説明があってそこに入り込んだまま抜け出せず、結局超実数がなんなのかわかったようなわからない状態になります。 そこで、超実数についての概略を超簡 […]
数列の「自明な収束」と「自明でない収束」
数列の収束には、自明な収束と、そうでない収束（狭義の収束）の２種類があります。 これらは明確に区別されますが、どちらもひとくくりに収束と呼ばれるため、場合によっては混乱する場合があります。
関数√tan(x)を微分するとこうなる
関数\(\sqrt{\tan(x)}\)の微分です。 関数\(\sqrt{\tan(x)}\)の微分(導関数) \(\sqrt{\tan(x)}\)の微分は、 \(\sqrt{f(x)}\)の微分公式を使って計算します。
